神奇的锁定放大器（Lock-in Amplifier）

前言

最近在CNPP同学处嫖到一片ADI公司生产的 AD630 ，这是一款平衡调制/解调器IC，有非常多的用途，其中之一就是锁定放大器，具体作用体现在——它能从相对于信号100dB的噪声中恢复出被噪声淹没的信号!

100dB是什么概念呢?

20\lg{S} = 100dB

S = {Vpp(noise)\over{Vpp(Signal)}} = 10^5 = 10万倍

比如…我的信号Vpp为10uV，噪声的Vpp为1V，这时S就是100dB。而AD630 据说（可不是瞎说，他Datasheet上标的…） 能将我的信号从这汹涌的噪声洪流中将它还原出来…

这不得来试一试？

锁定放大器(Lock-in Amplifier-LIA)基本原理

此处参考杨建国老师编著的《新概念模拟电路》-信号处理电路分册的 Section130.电荷放大器与锁定放大器 （yjg我的超人!）

数学原理

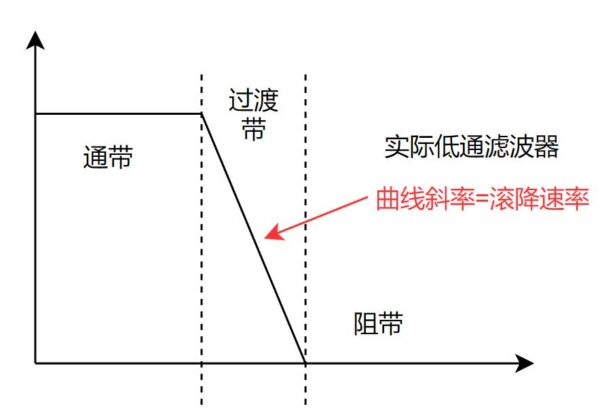
在微弱信号检测领域，遇到的最大问题就是被测信号往往都被淹没在广谱的噪声之中。此时如果想要从广谱噪声中提取指定频率的待测信号（一般为正弦），可以用模拟带通滤波器，也可以用数字带通滤波器。但这对带通滤波器的设计提出的极为苛刻的要求——通带无法做到很窄。

这就是锁定放大器出场的时候了。它的基本思想为:

1. 我有一个和待测信号同频率的正弦波，称为参考信号
2. 将参考信号与含有广谱噪声的待测正弦波相乘（使用乘法器）
3. 乘法器的输出得到一个含有直流分量的2倍频正弦波（相对于参考信号2倍频）
4. 这个2倍频信号的直流分量与待测正弦波幅度成正比，与两个正弦波相移有关。
5. 如果用低通滤波器滤除这个2倍频，只保留直流分量，就可以得到一个正比于待测信号幅度的直流量

来看看数学层面的解释（三角函数积化和差）:

A_{m1}\sin{(w_1t+\phi_1)} * A_{m2}\sin{(w_2t+\phi_2)} = \\
0.5A_{m1}A_{m2}\cos{((w_1-w_2)t+\phi_1-\phi_2)} - \\
0.5A_{m1}A_{m2}\sin{((w_1+w_2)t+\phi_1+\phi_2)}

如果w1=w2=w（频率相同），则有:

A_{m1}\sin{(wt+\phi_1)}*A_{m2}\sin{(wt+\phi_2)} = \\
0.5A_{m1}*A_{m2}\cos{(\phi_1-\phi_2)} - \\
0.5A_{m1}*A_{m2}\sin{(2wt+\phi_1+\phi_2)}

如果再进一步,有 \phi_1=\phi_2=\phi 则有:

A_{m1}\sin{(wt+\phi)}*A_{m2}\sin{(wt+\phi)} = \\
0.5A_{m1}*A_{m2} - 0.5A_{m1}*A_{m2}\sin{(2wt+2\phi)}

此时我们就可以从这个关系式得出如何求解待测信号了。待测信号为:

A_{m2}\sin(wt+\phi)

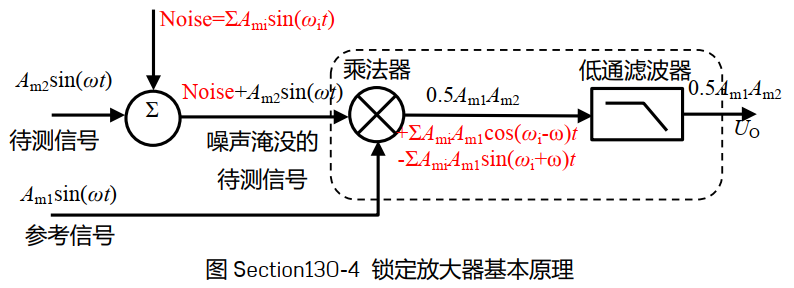
要求Am2,那么就做一个与他同频率，同相位，幅度为Am1的参考信号，将它们两个塞进乘法器相乘，得到最后的公式结果。其中第一项为直流分量，第二项为2倍频信号。

再用低通滤波器滤除2倍频信号，就可以得到0.5Am1Am2的大小了。Am1已知，求Am2不是有手就行?（诶我手呢?）

额外的优点

上式还有额外的功效——经过低通滤波后，可以保留与参考信号频率相同的待测信号，剔除全部与参考信号频率不同的量。这也可以从数学角度出发得出:

如果w2 != w1 （抱歉C写多了hhh），那么乘法器输出仍然为两项，但是第一项不再是直流分量，而是一个低频正弦波:

0.5A_{m1}A_{m2}\cos((w_1-w_2)t+\phi_1-\phi_2)

此时乘法器输出无直流成分。那么经过低通滤波器之后，输出一定为0。这导致锁定放大器输出经过低通滤波之后，广谱噪声均被剔除，而只保留了待测信号。

但是实际情况可能这样吗？当然是不可能的。杨老师在书中没分析，我自己想了一下原因应该如下:

• 低通滤波器不理想。与参考信号频率相差非常小（甚至同频率）的噪声所产生的交流成分的频率很低。
• 而低通滤波器很难做到极低的截止频率，又同时又具有极低的群延迟 (更正:不关群延迟的事，我概念记歪了，这里应该考察低通滤波器的输出建立时间，感谢小白指正)。这会导致低通滤波器的输出会有微弱起伏。

理想锁定放大器的困境

上述的锁定放大器理论分析，全部建立在一个重要的基础上:

参考信号与待测信号同频同相

但在实际工作时，要达到这个条件并不容易，甚至十分困难。如果不能保证他们同相，那么不知道相位差，要通过输出直流量求解原信号就无从实现。

好在还是有解决办法的。

Solution1:在参考信号通路中加入移相环节

利用cos（0）=1而cos（phi）< 1，在参考信号通路中加入移相环节，不断手动或自动调节相位，总能找到输出直流量的最大值。此时相差一定为0°，也就是参考信号与待测信号同相。

but，这种方法非常麻烦。

Solution2:双相位法

这种方法能一次性求解出Am2，同时获得2信号相位差。但方便的同时也会付出额外的代价——电路系统变得更加复杂了（虽然看起来复杂了，但实际上可能并没有，之后会说）

双相位法需要制作2个参考信号，他们同频率且存在90°的相移。

设待测信号为： A_{m2}\sin(wt+\phi_2)  \\
参考信号A为 : A_{m1}\sin(wt+\phi_{1A}) \\
参考信号B为 : A_{m1}\sin(wt+\phi_{1B}) 

用2个完全相同的乘法器，他们的乘数相同，均为被噪声淹没的待测信号，他们的被乘数为2个相互正交（相差90°）的参考源，这样得到2个乘法器的输出，经过相同的低通滤波后，输出分别为:

U_{OA} = 0.5A_{m1}A_{m2}\cos(\phi_{1A}-\phi_{2}) \\
U_{OB} = 0.5A_{m1}A_{m2}\cos(\phi_{1A}-\phi_{2}+{\pi\over 2}) = 0.5A_{m1}A_{m2}\sin(\phi_{1A}-\phi_2)

利用 \sin^2(\alpha)+\cos^2(\alpha)=1 的特性，将上述2个输出信号实施平方和开根号运算，得到:

U_O = \sqrt{U^2_{OA} + U^2_{OB}}=0.5A_{m1}A_{m2}\sqrt{sin^2(\phi_{1A}-\phi_2)+\cos^2(\phi_{1A}-\phi_2)} = 0.5A_{m1}A_{m2}

至此，我们无需知道待测信号与参考信号的相位关系，就可以获得待测信号的幅度。
同时可得出参考信号与待测信号的相位差:

\tan(\phi_{1A}-\phi_2) = {\sin(\phi_{1A}-\phi_2)\over\cos(\phi_{1A}-\phi_2)}={U_{OB}\over U_{OA}} \\
\phi_{1A}-\phi_2=tan^{-1}{U_{OA}\over U_{OB}}

实际上，如果不要最后一步的平方和开根号，保留前面的所有电路，这种解调方法也被称作 相干解调（Coherent demodulation），或者是模拟相干检波，广泛用于通信接收电路中（比如雷达接收机）。

但这种电路有一个缺点就是——乘法器的作用是对输入信号进行 混频。信号与系统中学过的知识告诉我们，时域信号 相乘，在频域中体现为 卷积，意思就是说对乘法器的2个输入信号的频谱进行卷积操作，得到的结果就是输出信号的频谱（理想乘法器，在实际的器件中会存在非线性失真）。而混频的后果就是可能会产生 镜像频率，简称 镜频。

如果镜频的频率落在LPF（低通滤波器）的通带内，那么这个镜频不会被滤除，这样就为后续信号的进一步处理带来了误差。当然这都是题外话了（233一不小心扯远了）。

从理论到实践——方波作为参考信号

上述所讲述的相干解调方法实现起来可真不容易呢…最大的难点在于 精准的90°移相。我们知道全通滤波器可以实现对模拟信号的移相，但是它的相频曲线并不是一马平川的，输入信号的频率不同，全通滤波器对其的移相大小也不一样。在模拟电路中实现对全频段信号的移相固定为90°，且输出幅度不变还是很困难的。

另外一点就是 模拟乘法器实在是太贵了！
感兴趣的读者可以搜一搜ADI公司的模拟乘法器比如AD835/AD834这样的，了解一下市场行情。

实践中，多半使用方波作为参考信号实现锁定放大。原理如下:

1. 使用占空比为50%的正负方波, 其幅度为A_{m1},角频率w，相移为 \phi_1

表达式为:

U_{REF}(t) = \left\{ \begin{array} {c} A_{m1}; {\phi_1 \over w}\leq MOD(t,T={2\pi\over w})<{\phi_1 \over w}+{\pi \over w} \\ -A_{m1}; MOD(t,T={2\pi\over w}) < {\phi_1 \over w}; and\,MOD(t,T={2\pi\over w}) \geq {\phi_1 \over w}+{\pi \over w} \end{array} \right.

2. 此方波与频率相同，相位相同的正弦波相乘，会出现如下图所示的波形。

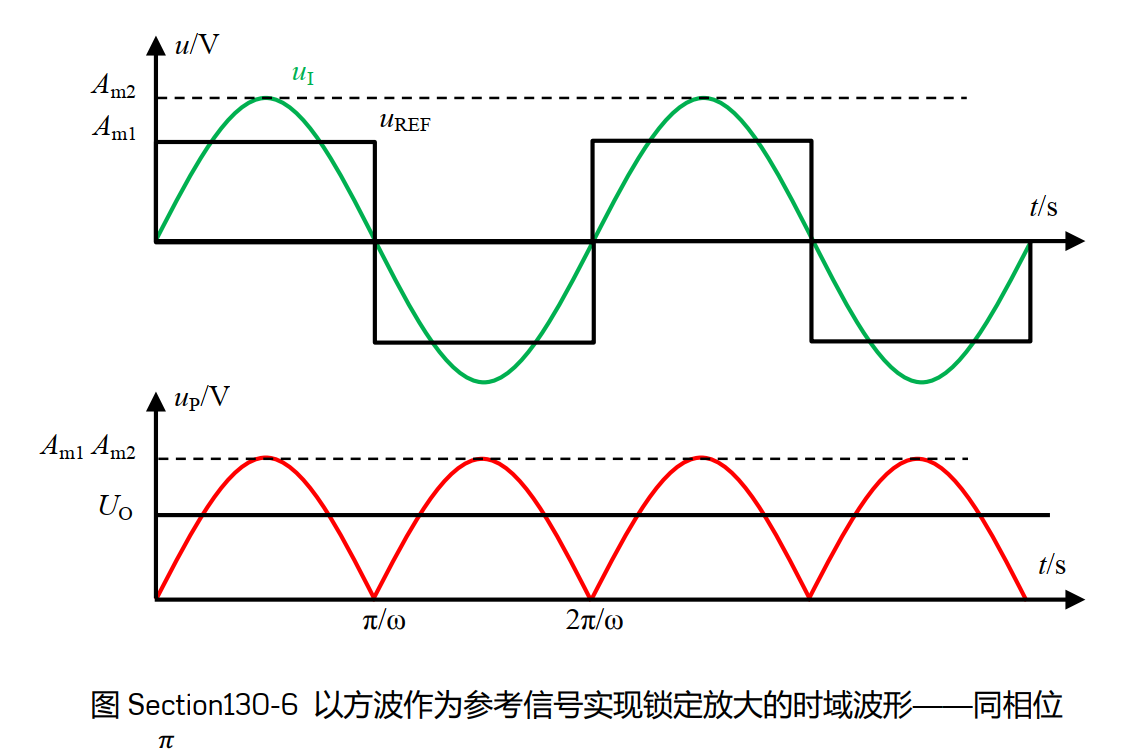
其中，Up为乘法器的输出波形（红色曲线），经过低通滤波后得到直流分量（即波形的平均值）为Uo，这可以通过对波形进行半个周期的积分除以半个周期得到:

U_o={1\over {\pi \over w}} \int_0^{\pi \over w} {A_{m1}*A_{m2}\sin(wt\,dt)} = {2 \over \pi}A_{m1}*A_{m2} \approx 0.6366A_{m1}*A_{m2}

3. 当以待测波形0度相移，而参考波形具有 \phi_1 相移，可以得到Section130-7所示如下的时域波形:

可以看出乘法器输出波形仍是 周期性的，其周期为待测波形周期的2倍。同样，也可以利用半个周期积分除半个周期的方法得出乘法器输出平均值，也就是低通滤波器输出Uo:

U_o = {1\over \pi} \int_{\phi_1}^{\phi_1+\pi} A_{m1}*A_{m2}\sin(wt)\,d(wt) = {2\over \pi}A_{m1}*A_{m2}\cos \phi_1 \approx 0.6366A_{m1}*A_{m2}\cos \phi_1

由此可知，当2信号同频但存在相移时，低通滤波器输出正比于两信号的幅度乘积，且相移越大输出越小（cos关系），直至相移90°时输出为0，相移大于90°时输出小于0，相移180°时输出为负值最大。这个结论与 以正弦波为参考信号完全相同，他们唯一的区别是参考信号为方波时，最大值不再是0.5Am1xAm2，而是0.6366Am1xAm2。

4.当待测信号与参考信号频率不同时，可证明乘法器输出是一个 正负对称信号，经过低通滤波之后输出一定为0.

说到这里，我们可以把乘法器扔一边去啦~

用方波作为参考信号实现锁定放大的好处如下:

• 1.不用再用贵上天的乘法器了！我们可以使用 模拟开关 和反相器来实现锁定放大，结构如下:

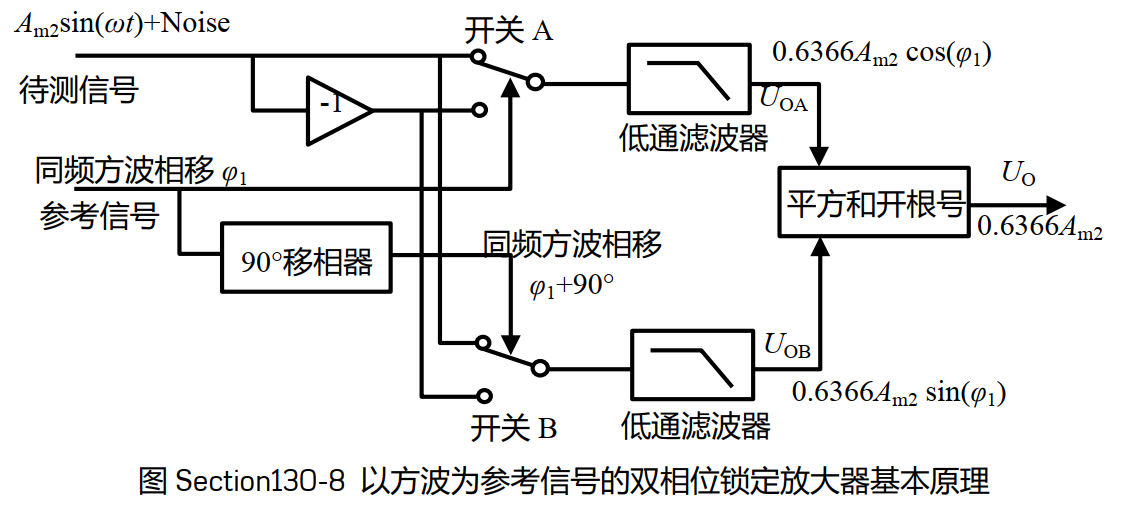
• 2.对方波信号进行90度移相还不简单？上图中方波用于控制开关的导向，因此只需要是数字电平的0&1即可。这样就完全可以使用数字电路来控制。用数字电路产生90°相移，可以用单片机、FPGA、触发器等完成，方法很多。

LIA的用法？

码字好累呀，偷个懒抄书——

至于为什么2个信号源的频率会漂？了解DDS的同学都知道（如果不了解可以看我 上次写的文 嗷）多半是信号源的时钟源不稳定导致的。比如该时钟源的频率会随着环境温度、湿度、承受的电压、时间等因素而发生微小的漂移，从而导致DDS的输出频率有微小的变化。虽然在示波器上基本看不出来，但对锁定放大器来说这些误差还是十分可观的。

因此多数情况下LIA都工作在下图所示的模式下。

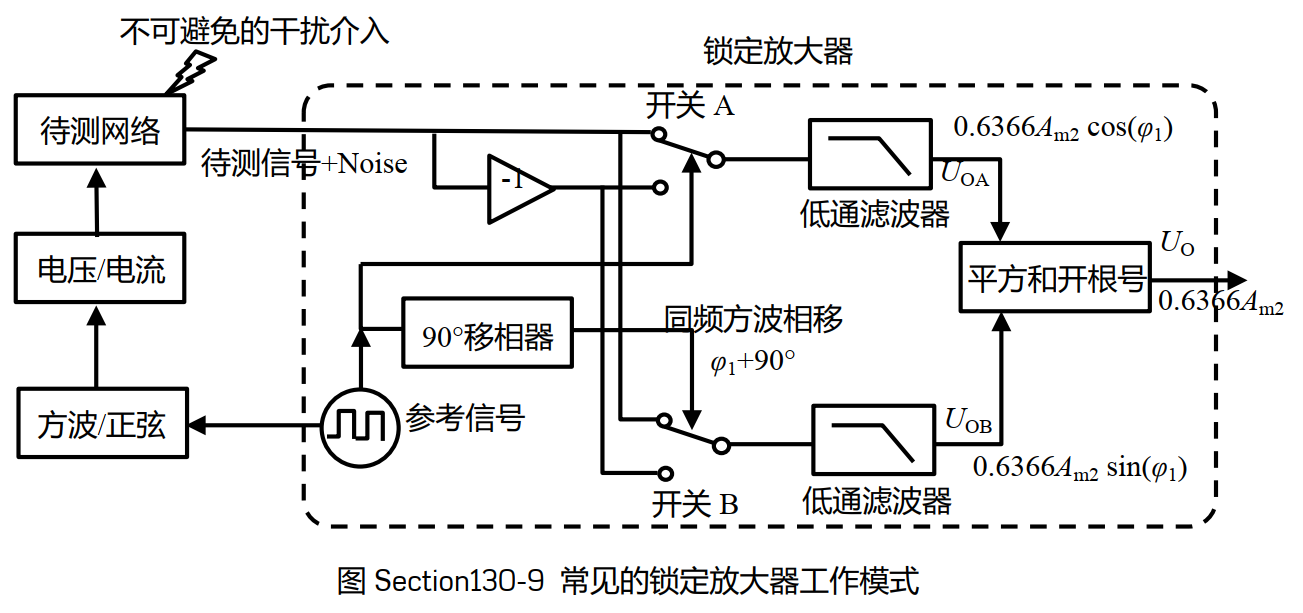
图中一切信号的频率源在参考信号，它在给锁定放大器提供参考频率的同时，还给待测网络提供测试信号，因此一定能够保证待测信号的频率与参考信号的频率完全一致。（我同一个信号在传递的过程中频率总不可能漂了吧（

图中 方波/正弦 是将参考信号的方波变换成同频正弦波，可用带通滤波器等方法实现，当然也可以用正弦当频率源，将正弦转为方波作为参考信号。

使用比较器+模拟开关实现LIA

双相位法可以用方波作为参考信号，那么不用双相位法的LIA可不可以用方波作为参考信号实现呢？当然是可以的。

为了验证，我使用LTSpice搭建了一个仿真电路，原理图如下:

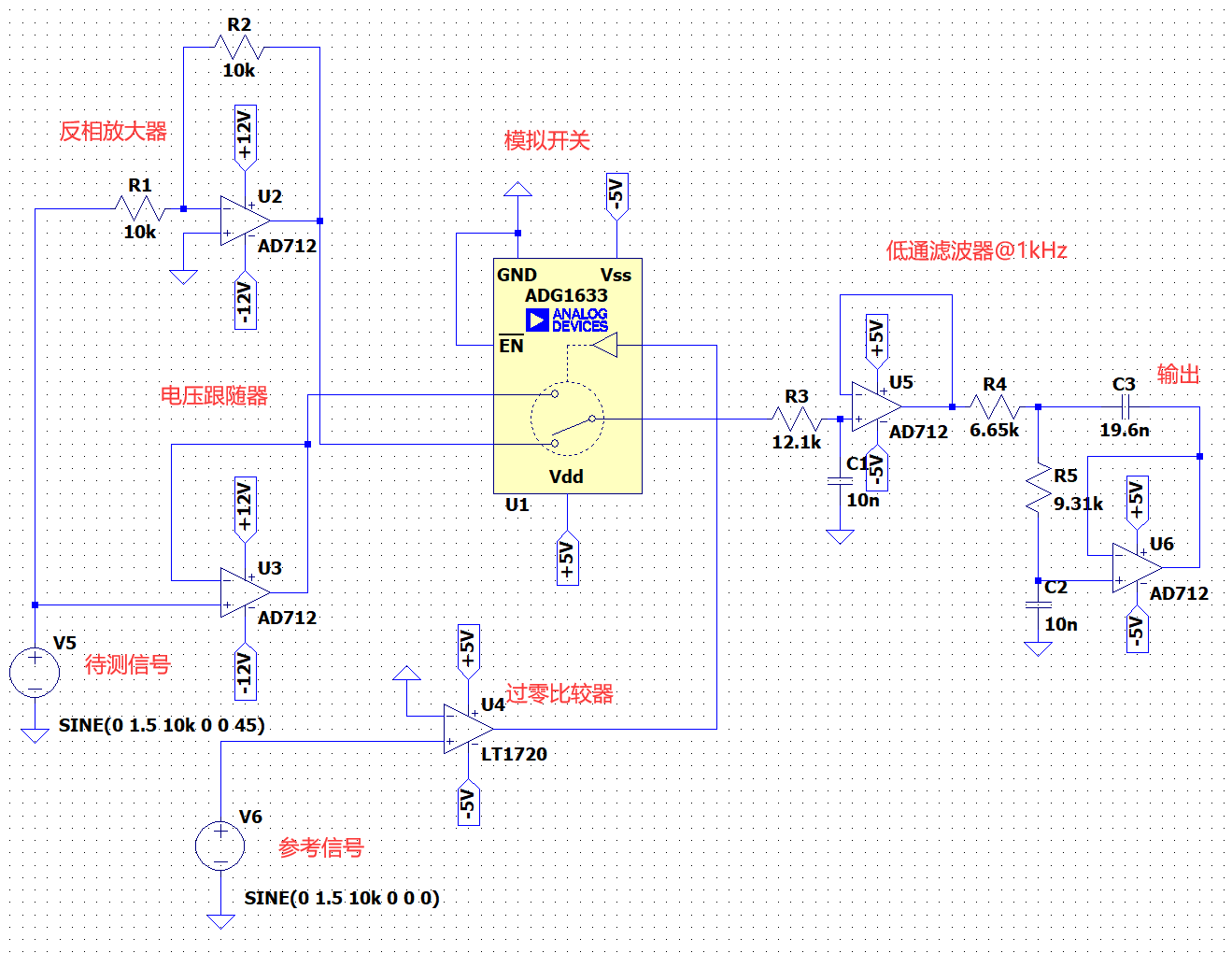
待测信号与参考信号同频率（都是10kHz），但是存在相差。2个信号都是正弦，参考信号经过过零比较器后变成方波，用于控制模拟开关ADG1633的选通。模拟开关的输入一个为待测信号，另一个为反相的待测信号（相移180°）。模拟开关的输出经过一个截止频率为1kHz的低通滤波器，输出直流信号，测量这个直流信号来验证方案可行性。

如果前述计算正确，那么输出直流电平应该有如下关系（待测信号幅度1.5V）:

0.6366*1.5*cos(\phi) \\
when \phi = 0\degree, \,V_{DC}=0.9549V \\
when \phi = 45\degree, \,V_{DC}=0.6751V \\
when \phi = 90\degree, \,V_{DC}=0.0V \\
when \phi = 180\degree, \,V_{DC}=-0.9549V \\

仿真结果:

• 180度相移

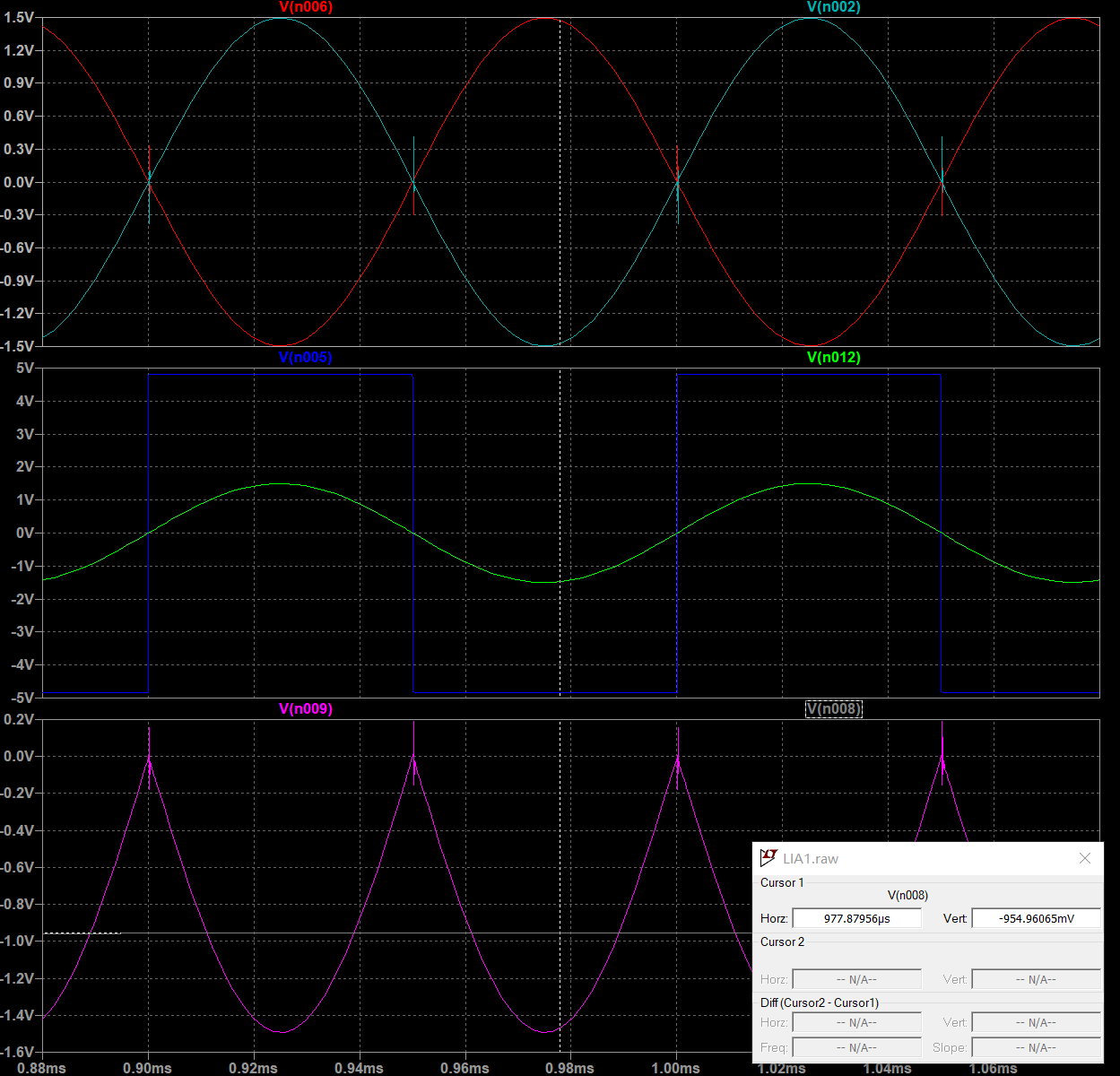
• 90度相移

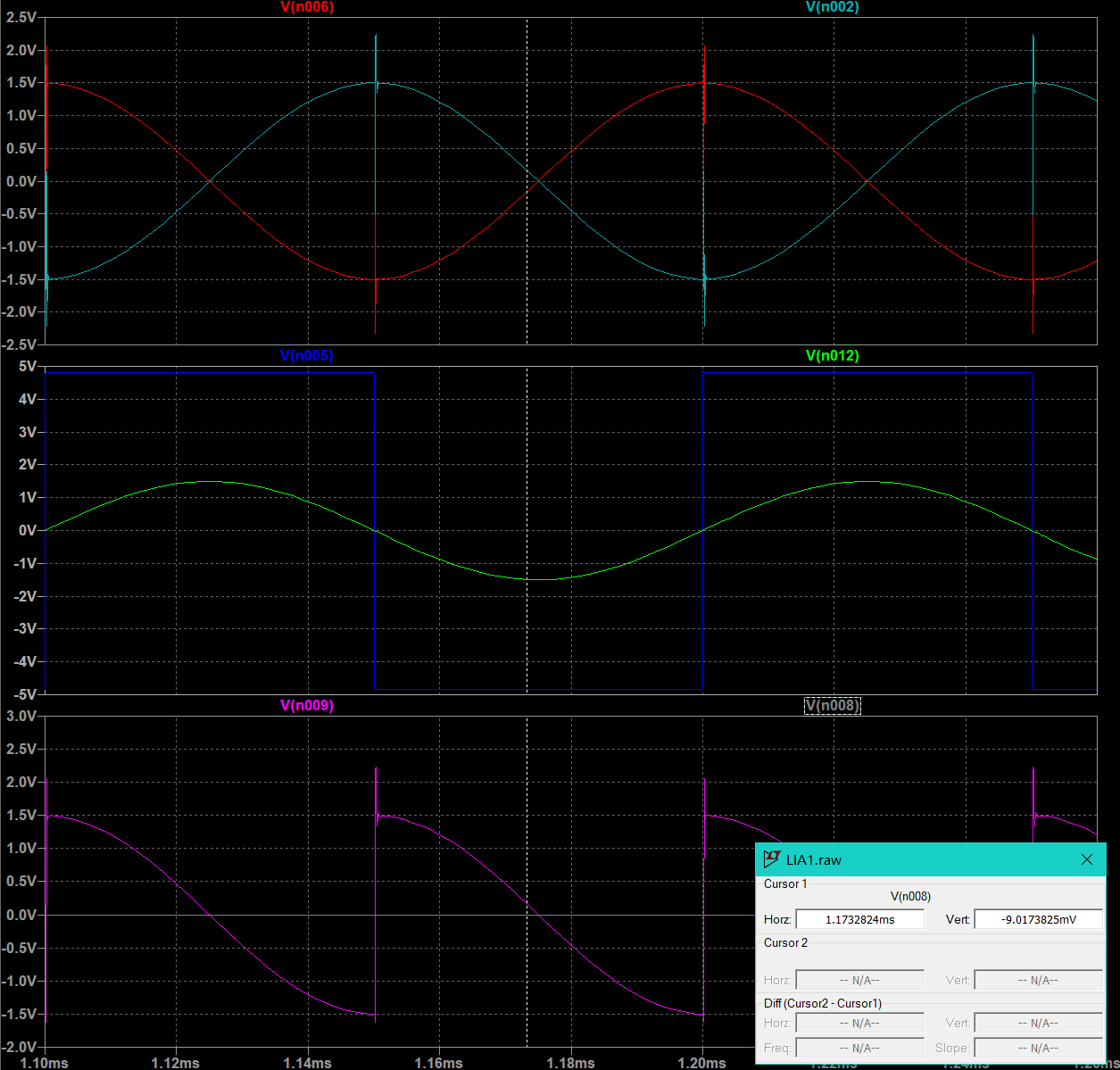
• 45度相移

• 0度相移（同相）

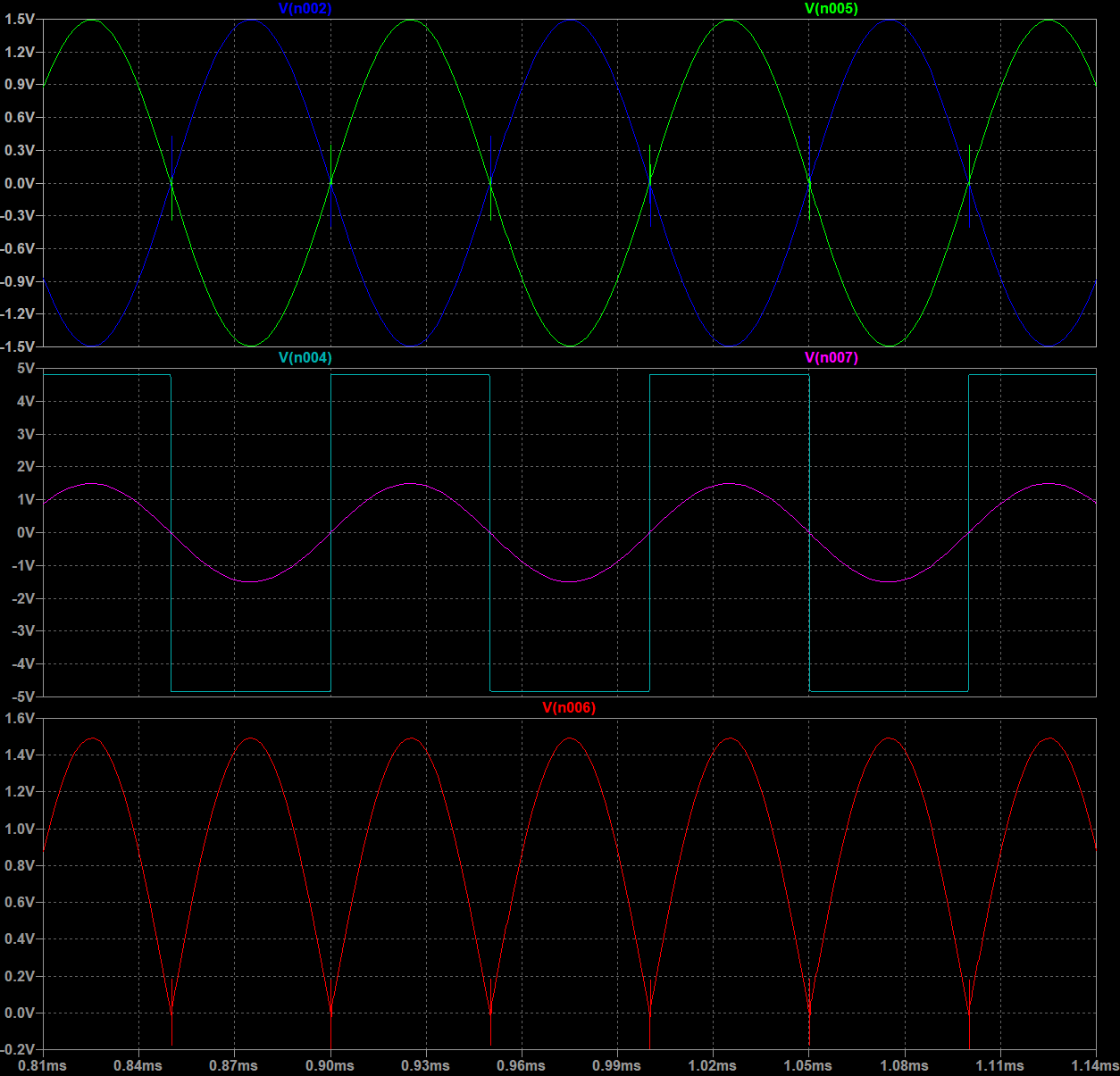
嗯，考虑到各级电路的失调电压、偏置电流等影响，还有模拟开关导通关断瞬间产生的尖峰，可以说结果是非常理想了。

AD630

AD630可用作锁定放大器，在datasheet中关于LIA的用法介绍如下:

还给出了一个电路图，长这样：

我们来分析一下~

左下的信号是一个0.1Hz调制信号，载波频率为400Hz，同时输出了载波的同频同相参考信号，加到了AD630的9脚，为其内部的模拟开关提供选通参考。

这个调制信号经过了他头上的 Attenuator（衰减器） ，衰减倍数是100dB...也就是...呃...10万倍。如果信号原来的Vpp是1V，那么衰减过后只剩下了10uV。

再来看最上面的 Clipped Band Limited White Noise ，这个是 带限白噪声 ，可以用一个广谱的白噪声经过一带通滤波器之后得到。

现在有了噪声信号和衰减过的信号，我们用反相加法器将他们加起来（反相加法器的特点是源间隔离，互不干扰）。然后输入到AD630的1脚。

AD630内部的结构挺简单，但这个电路图画的非常绕，看的人脑阔疼...我简单分析了一下，直接给出结果：

• 在模拟开关选通 上通道/下通道 的时候，AD630内部放大器对输入信号放大分别为 2倍/-2倍 ,就跟我上面拿LTSpice仿真的结构类似，不同的是AD630的输出接了补偿电容，还有一个未知的补偿网络。
• 输出经过一个反相放大器之后再经过一RC低通滤波器，得到解调之后的输出信号。

可以看上面截图中的 Figure.34，加上噪声的信号已经完全分辨不清原来的形状了...但通过LIA能将它还原出来，就挺神奇的。

试一试呗

为此我画了个板子，电路图就是上图手册中的那个，用覆铜板热转印制作了这块PCB。

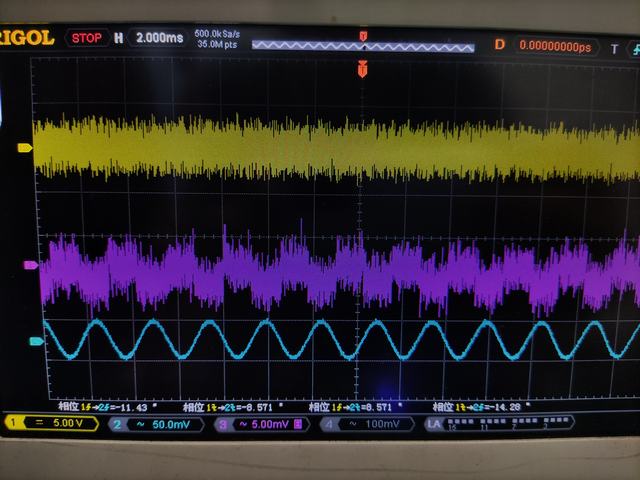
测试输入信号使用一个AM调制信号，幅度比较低，然后加上信号源输出的Noise信号，幅度比较高，使用调制信号的Sync信号作为AD630的载波相位参考信号，加上双12V电源，测试输出如下:

可以看到还是能还原大致的形状的~不过似乎远没有官方手册中所说的那样凶猛的性能，能从100dB的噪声中恢复信号...

又尝试了另一个调制信号，这次将信号幅度缩小了10倍多，得到输出长这样...好吧有点不忍直视了，如果把带宽限制打开或许会好看一点...

Plan

我预计会画一个锁定放大器的PCB，专门用来做LIA，可以用作高频LCR电桥的模拟前端。

这期就到这里啦。电赛推迟了才闲下来写了这篇文。之后会写更多的技术总结文章的~

敬请期待！