本文目录
基础模拟与数字调制技术
本文承接上次的 深入理解DDS(数字频率合成) 一文,继续探讨在通信系统中占据核心地位的 调制(Modulation) 技术。
在网上搜集资料时没找到什么特别好的资料,于是就打算从上次的 [DDS Technical Tutorial] 的 Section 9. Basic Digital Modulator Theory 开始,继续意译,辅助以Wiki百科和各类通信原理和射频电路参考书籍上的内容来讲解。
sorry,我仔细看了那篇教程后发现其并不是特别适合写这篇文。那么我就从Wiki和各种参考书和教材上搜集资料了。
Working List
- AM
- FM
- PM
- ASK
- FSK
- PSK
- 特殊信号
- 高阶调制 鸽鸽还在咕😭
- 其他
为什么要调制?
如果我们想通过电信号传输一些信息,我们可以选择使用导体介质并加载模拟信号或数字信号来完成——前者比如AV电视,后者比如SPI、UART协议等。但这些传输都有局限性: 它们不能传输很远的距离,且一般来说通信频率越高距离越短。
那么我们来换一个思路,使用无线通信技术(Wireless Communication)。通过电磁场理论和天线原理我们可以知道,如果要发送一个特定频率的信号,我们需要一个 物理尺寸与之波长的数量级相当的天线(Antenna)。如果我们要发送语音信号,一般语音信号的频段为10Hz~20kHz,其对应天线长度约为几十甚至上百千米,显然这不现实。
如果我们想个办法,将信号的频率大幅提高,提高到MHz甚至GHz数量级,那我们就能制作合适的天线来完成该信号的发射了。理所当然地, 调制(Modulation) 技术就应运而生了。调制的实质就是使 相同频率范围的信号分别依托于不同频率的载波上,接收机就可以分离出所需的频率信号,不致互相干扰。 这也是在同一信道中实现 多路复用 的基础。
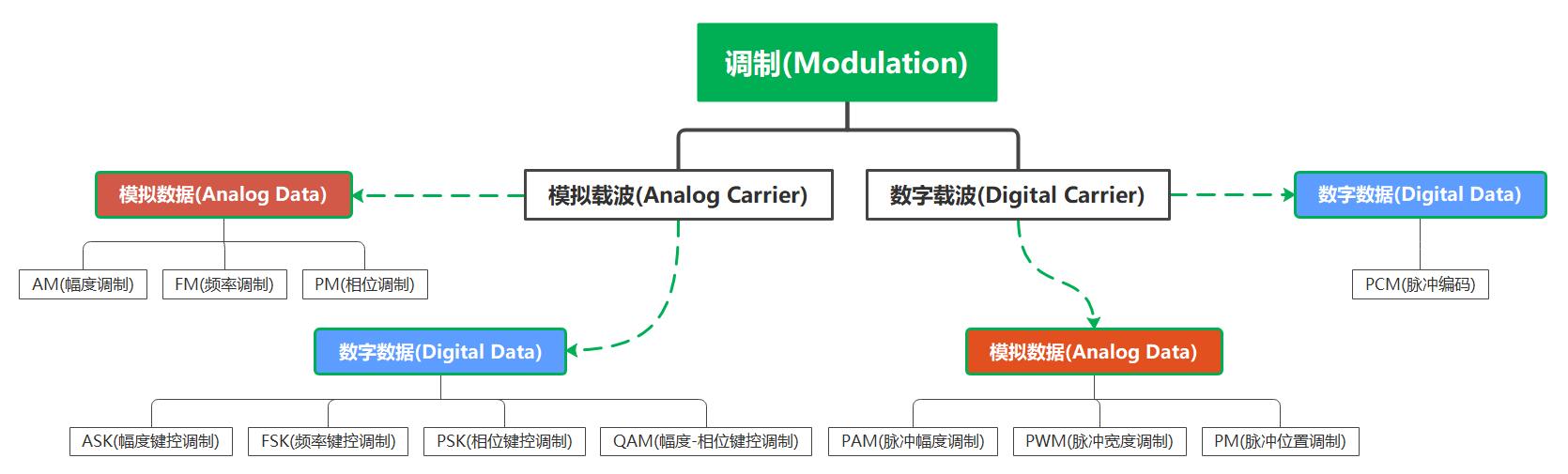
就像我们去很远的地方会乘坐交通工具一样,信息也能乘着 高频电磁波 传播到更远的地方~,不过在工程中我们不会说信号上了什么泥头车,我们会说含有信息的信号 被调制 到 载波(Carrier) 上了。以下是一些术语辨析:
| Name | English | 意义 |
|---|---|---|
| 基带信号 | Baseband Signal | 我们要传送的信息信号 |
| 载波信号 | Carrier Signal | 带着基带起飞的信号 |
| 调制 | Modulation | 基带信号 "登机" 的过程,在发送端完成 |
| 信道 | Communication Channel | 信号在通信系统中传输的通道,可有线可无线 |
| 解调 | Demodulation | 基带信号 "下机" 的过程,在接收端完成 |
其中,基带信号如果是模拟信号,那么我们就称其为 模拟基带,数字的就是 数字基带。在无线通信系统中我们多半使用模拟载波,所以我们接下来针对模拟载波的调制一一解剖一下。
一.模拟调制
模拟调制是最早应用的调制技术。早在20世纪初无线电刚刚问世时,就有工程师成功地利用模拟调制技术实现了远距离无线通信。
1.1 AM(Amtitude Modulation)
幅度调制顾名思义,就是让载波的幅度跟随基带信号的幅度变化,它在20世纪头二十年间发展,在今天,它仍在多种通信形式中使用;例如用在便携式对讲机、VHF航空无线电、民用波段无线电、短波电台与电脑的调制解调器中。
下图展示了调幅信号的完整信号链,从左至右依次为: 模拟基带信号、载波信号、已调信号及其包络线、实际发送的信号波形、接收端接收到的信号波形、接收端接收到的信号的包络线、包络检波(解调)出来的信号。

1.1.1 数学形式
载波信号频率为 f_c,幅度为 A:
c(t) = A\sin(2\pi f_c t)令 m(t) 表示调制波形(基带信号),载波的频率比基带的频率要高得多:
m(t) = M·\cos(2\pi f_mt + \phi)其中 M 是调制的幅度,我们需要让 M<1 以使 1+m(t) 总是正数。若 M>1 则会出现 过调制,从传输信号中重构基带信号会导致原始信号的丢失。AM的最终结果就是载波 c(t) 乘以正数 1+m(t) 。
y(t) = [1+m(t)]·c(t) \\
= [1+M·cos(2\pi f_m t + \phi)]·Asin(2\pi f_c t)运用积化和差恒等式, y(t) 可以用3个正弦波的和表示:
y(t) = A·\sin(2\pi f_ct) + {AM \over 2}[\sin(2\pi(f_c+f_m)t + \phi) + \sin(2\pi(f_c-f_m)t - \phi)]因此,调制信号有 3个组成成分:
- 载波
c(t) - 频率略高于载波频率的 上边带(upper-band)
- 频率略低于载波频率的 下边带(lower-band)
其频谱结构如下图所示,请注意我们在上面的推导中仅仅使用了 单频基带信号 ,因为这样便于看清楚数学表达形式。实际的基带信号的频谱绝不是一个单一值,而是具有一定"宽度"的,经过调制后其上下边带同样是具有一定宽度的,就像图中那样:

上面是单边谱,下面是双边谱,看上面的就行
然而,真正携带信息的只有上下两个边带成分, 载波本身并不携带信息。所以标准AM调制的频谱利用率和效率并不高。
1.1.2 调制系数与失真
在上面的推导式中,M此处与 调制系数(Modulation Index) 相同,调制系数表示调制变量在未调制水平附近变化的范围,其定义式为:
m = {m(t)的峰值 \over A}={M \over A}通常调制系数 m 以百分比作为单位,如果 m=50\%,载波信号的幅度在其未被调制的幅度上(下)变化50%。如下图所示第一种情况。如果 m=100\%,就是第二种情况,这时已调信号的包络线会降到0,也即意味着 完全调制。通常为了获取理论上最高的信噪比,我们希望调制系数 尽可能接近1但是不能超过1。一旦调制系数超过1,就出现了 过调制(Over modulation) 现象(下图第三种情况)。因为包络的负偏移不能小于0,所以会导致接收到的调制信号 失真(distortion),形象地说,是被 "削波"了。

我写了一段python代码,可以生成标准AM调制信号,如果你感兴趣可以看看:
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from cycler import cycler
N = 4000 # 采样点4000点
f_baseband = 1e2 # 包络频率100Hz
f_carrier = 1e3 # 载波频率10kHz
# 时间间隔
t = np.linspace(-2/f_baseband, 2/f_baseband, num=N)
# 生成包络与载波信号
baseband = np.sin(2 * np.pi * t * f_baseband)
carrier = np.sin(2 * np.pi * t * f_carrier)
# 调制系数m
m = 1.0
# Plot
fig, axd = plt.subplot_mosaic([['upleft', 'right'],
['lowleft', 'right']], layout='constrained')
axd['upleft'].set_title('baseband signal')
axd['upleft'].plot(t, baseband, 'k')
axd['lowleft'].set_title('Carrier signal')
axd['lowleft'].plot(t, carrier, 'k')
axd['right'].set_title('Modulated signal')
axd['right'].plot(t, (1+m*baseband)*carrier, 'k')
axd['right'].legend()
# show
plt.show()
我还在网上找到一个非常巧妙的标准AM调制电路图,它利用同相放大器和 FET的近似线性电阻区 特性,将FET当作一个跟随调制信号幅度动态线性变化的可变电阻,从而改变了同相放大器的增益,实现了标准AM调制。
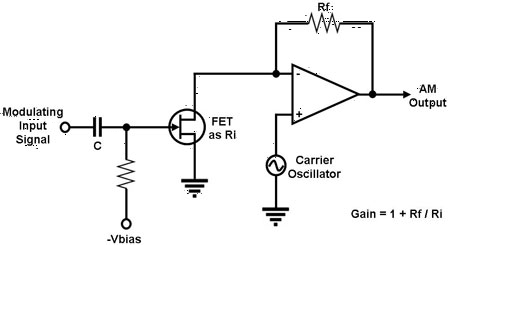
1.1.3 AM的优缺点
调幅是历史上最早发明的调制方式。调幅的优点是 容易产生及恢复信号(说白了就是便宜!) 。在发射器中,可以用交换调制器,或是平方率调制器(square-law modulator)来完成调制。在接收器中,可以用包络检波器,或是乘积检波器(product detector)来完成解调。也就是说,调幅系统成本十分低廉,这就是为什么AM无线电广播会如此受到欢迎。
当然便宜的方法多数情况下都有那么些重大缺陷,AM也不例外。AM的缺点有二:
- 浪费功率(效率低)
载波c(t)与带有信息的基频信号m(t)并不相关。因此,传输载波就会浪费功率,也就是说,在调幅的总功率中,有一部分是真正有被m(t)影响,有另一部分是被浪费的。 - 浪费带宽(频带利用率低)
AM波的上边带及下边带相互对称于载波频率,所以若我们知道其中一组边带的幅度谱及相位谱,由于对称性,我们就可以知道另外一组。这也表示在信息传输的时候,其实只有一组边带就够了,因此信道也只需要提供等同于基频信号的带宽,这样来看,因为调幅需要的传输带宽是信息带宽的两倍,所以我们可以称它是 浪费带宽的。
那么有没有办法改进捏?当然是有的~
不过需要付出代价!(Money--,系统复杂度++)
1.1.4 AMの超进化
经典的主流方案有3种:
- 双边带抑制载波调制(DSB-SC,=Double-sided band-Suppressed carrier)
DSB-SC的发射波只由上下边带组成。因为抑制了载波,所以可以节省传输功率,但是信道带宽需求还是跟原来一样,也就是信息带宽的两倍。 - 残留边带调制(VSB, =Vestigial-Sided band)
VSB调制让一组边带几乎全部通过,而另一组边带几乎全不通过,也就是有少量的残留。所以,VSB的带宽需求,比起信息带宽多了前述的残留边带的宽度。这种方式的调制,很适合用在宽频信号,比如说电视信号,在极低频率处含有显著的成分。又例如说,在电视广播中,很强的载波会跟被调波一起被发送,所以我们能在接收端处用包络检波器来解调信号,因此接收器的设计得以被简化。 - 单边带调制(SSB,=Single-Sided band)
SSB的被调波只由上边带或者是下边带组成,所以,SSB调制的功能是,将调制波的频谱在频域中转移到新的位置。单边带调制适合传送声音频号。这样的调制方法需要的传输功率以及信道带宽都最小,但缺点是实现成本的增加以及系统复杂度的增加(哪种改进都得增加orz)。
其实每种调制都能深挖一大堆出来...但是我怕文章写太长了,又写成 电子入门百科全书) 那种量级的...所以一些拓展内容(比如调制电路、解调电路、发射机、接收机电路等)就忽略了~
1.2 FM(Frequency Modulation)
调频(Frequency Modulation) 是一种以载波的瞬时频率变化来表示信息的调制方式。(与此相对应的调幅是透过载波幅度的变化来表示信息,而其频率却保持不变)在模拟应用中,载波的频率跟随输入信号的幅度直接成等比例变化。在数字应用领域,载波的频率则根据数据串行的值作离散跳变,即我们之后要讲的频率键控(FSK)。
调频技术通常运用在甚高频段(VHF无线电波段)上的高保真音乐和语音的无线电广播。普通的(模拟)电视的音频信号也通过调频方式传输。窄带形式的调频广播(N-FM)限于商业上的音频通讯和业余无线电领域,广播中使用的调频技术则一般称为宽带调频(W-FM)。
调频技术还用于大多数的模拟VCR,包括家庭视频系统VHS,用于记录视频信号的亮度(黑和白)信息,不过是在中频段使用。调频是用于录取视频磁带时唯一不造成大的信号走样的调制技术,因为视频信息的所包含的频谱范围很广,从几Hz到几十MHz,同均衡器工作时很难将噪声信息保持在-60dB以下。调频方式也使磁带处于饱和状态,起到降噪的作用,同时接收端的调频捕获效应基本消除了透印和前回声等现象。如果在信号上加上一个连续的导频音,就像在V2000以及许多Hi-band 格式上做的那样,机械抖动可以得到有效的控制,从而有助于时基校正。
调频技术还应用在音频的合成上,即所谓的调频合成,在早期的数字合成器上应用很普遍,并成为几代个人电脑声卡的标准特征。
AM和FM的区别
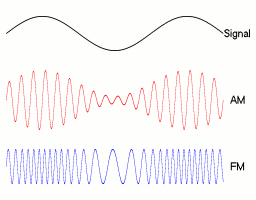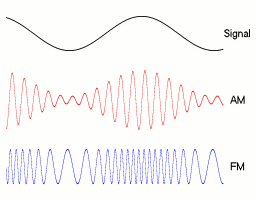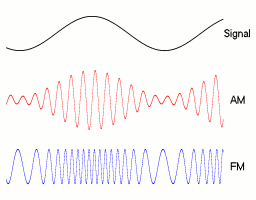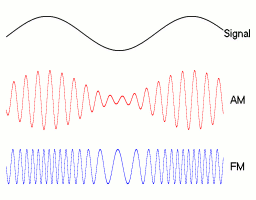
1.2.1 数学形式
如果基带信号为 x_m(t) 而正弦载波为 x_c(t)=A_c\cos(2\pi f_ct),其中 f_c 为载波的基频, A_c 是载波的幅度,调制器将基带数据信号与载波结合起来得到了已调信号(传输信号):
y(t) = A_c\cos(2\pi \int_0^t f(\tau) d\tau) \\
= A_c\cos(2\pi \int_0^t [f_c+f_\Delta x_m(\tau)] d\tau) \\
= A_c\cos(2\pi f_ct + 2\pi f_\Delta \int_0^t x_m(\tau)d\tau)上述公式中, f(\tau) 是振荡器的 瞬时频率, f_\Delta 是 频偏,代表在一个方向上相对 f_c 的最大频率偏移,在此我们假定 x_m(\tau) 的幅值限于 ±1 之间。
数学上,基带调制信号可以通过用频率为 f_m 的连续正弦信号来近似,这种方法也被称为单音调制,这个信号的积分就可以表示成:
\int_0^t x_m(\tau) d\tau = {\sin(2\pi f_mt) \over 2\pi f_m}这样就可以简化上述 y(t) 的表达式:
y(t) = A_c\cos(2\pi f_ct + {f_\Delta \over f_m} \sin(2\pi f_mt))其中,调制正弦曲线的幅度 A_m 通过 峰值频偏(frequency deviation,又称频率偏移) f_\Delta=K_fA_m 来表示。
正弦信号调制的正弦波载波的谐波分布可以表示为贝塞尔函数;这是在频域中频率调制的数学理解的基础。(🐟点进去看得云里雾里的...)来放一张图感受一下:
FM信号的频谱图(上部)+瀑布图(下部)
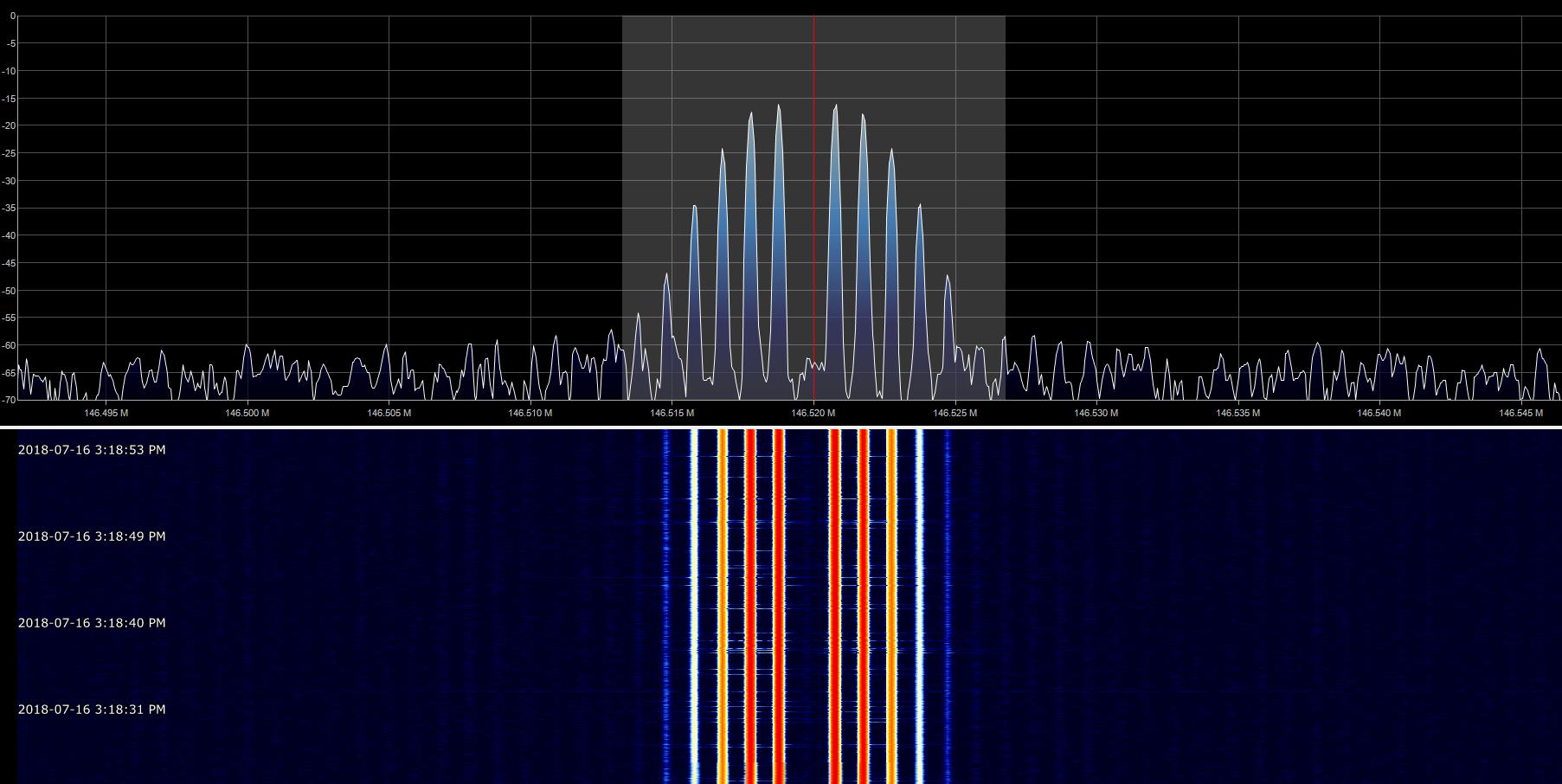
对于载波被单频正弦波调制的情况,已调信号的频谱可以用第一类Bessel函数计算得出。这个就不细讲了...🐟也搞不明白。
1.2.2 调制指数
和其他调制系统一样,调制指数表示调制变量在未调制水平附近变化的范围。它与载波频率的变化有关:
h = {\Delta f \over f_m} = {f_\Delta |x_m(t)| \over f_m}其中, f_m 是调制信号 x_m(t) 中出现的最高频率分量,而 \Delta f 是峰值频偏——即瞬时频率相对于载波频率的最大偏差值。对于正弦波调制,调制指数是载波频率的峰值频偏与调制正弦波的频率之比。
若 h\ll 1,则该调制称为 窄带调频(Narrow-Band FM, NFM),而其带宽约为 2f_m。有时 h \lt 0.3 被视为NFM,否则就是 宽带(Wide-Band FM, WFM)调频
对于 h \gg 1,那就一定是WFM了,此时其带宽约为 2f_\Delta。WFM在占用更多的带宽的同时能大幅提升信噪比(SNR)。比如说保持基频 f_m 不变,加倍峰值频偏 \Delta f,可以提升8倍的信噪比。
1.2.3 卡森法则(Carson‘s rule)
Carson's rule是一个经验法则,它指出了几乎所有的调频信号的功率 分布在带宽 B_T 内,这个带宽被称为 卡森带宽:
B_T = 2(\Delta f + f_m) = 2f_m(\beta + 1)其中 \Delta f 是从中心载波频率 f_c 到瞬时频率 f(t) 的峰值频偏, \beta 是调制指数,而 f_m 为调制信号中的最高频率。卡森规则的应用条件仅仅是正弦信号。对于非正弦信号:
B_T = 2(\Delta f + W) = 2W(D + 1)W 是调制信号中的最高频率,但本质上是非正弦信号, D 是调制非正弦信号的峰值频偏与最高频率之比。
1.2.4 FM调制解调方法
FM调制有直接和间接两种方式:
- 直接调制可以通过将基带信号接到一个 压控振荡器(Voltage-Controlled Oscillator, VCO) 来实现
- 对于间接调制,基带信号首先积分生成调相信号,用于调制晶体振荡器,得到的信号通过倍频器产生FM信号,此过程中生成的是窄带FM信号,随后再产生宽带FM信号,因此被称为间接调制...
解调方法有很多,例如锁相环电路就可以用于FM解调。通常的方法是 斜率鉴频(Slope Detection)。不过现在有很多IC直接集成了全部FM解调所需电路,十分方便~ 市面上很多FM收音机就是用的这种方案
1.2.5 FM的优缺点与有趣的应用
宽带调频(WFM)和调幅(AM)相比,在同样的调制信号作用下,宽带调频需要更宽的带宽。但是这也使信号具有 更强的抗噪声和干扰能力。调频还具有较强的抗简单信号幅度衰减能力( signal-amplitude-fading phenomena)因此,调频被选做高频、高保真无线电传输的调制标准。

FM具有比AM更强的抗噪声和RFI能力,在百万伏特电弧放电的环境下,AM接收机只能收到一片白噪声,而FM接收机却能清晰地解调出音乐(1940s, New York publicity demonstration by General Electric)
还有多普勒效应的应用~
还记得蝙蝠么?当回声定位蝙蝠接近目标时,其发出的声音以回声的形式返回,回声的频率是多普勒向上移动的(频率升高)。在某些蝙蝠种类中,产生恒定频率(CF)回声定位呼叫,蝙蝠在接近目标时通过降低呼叫频率来补偿多普勒频移。这使回波信号保持在正常回波定位呼叫的同一频率范围内。这种动态频率调制被称为 多普勒频移补偿(DSC,= Doppler Shifted Compensation)
1.3 PM(Phase Modulation)
相位调制(PM)和频率调制(FM)同属于角度调制的两种主要形式之一,它将消息信号(基带)编码为 载波的瞬时相位变化。PM中,载波的频率和幅度恒定,基带信号的瞬时幅度改变载波的相位。也就是说载波信号的相位被调制以跟随基带信号的变化。
相位调制是大量技术(如Wifi、GSM和卫星电视)背后的许多数字传输编码方案的一部分。
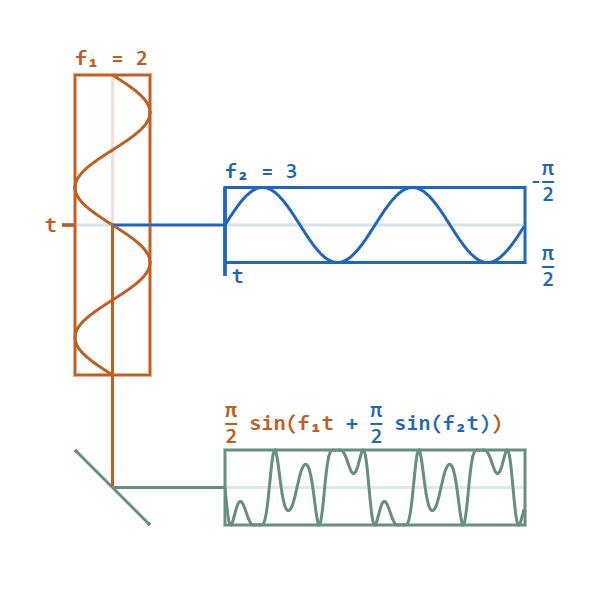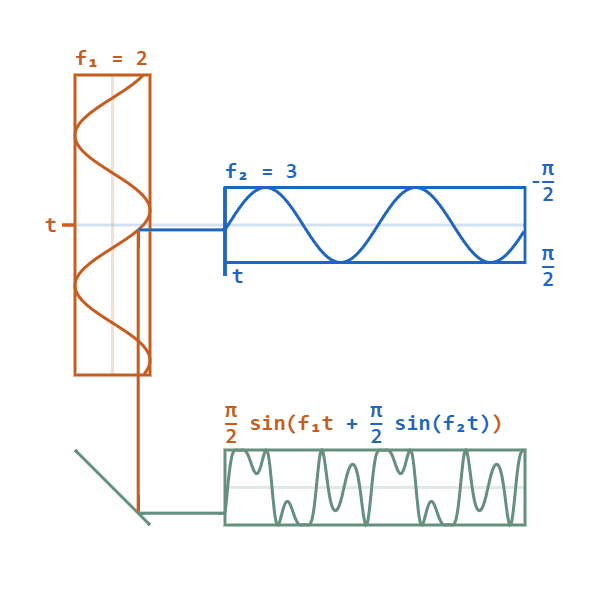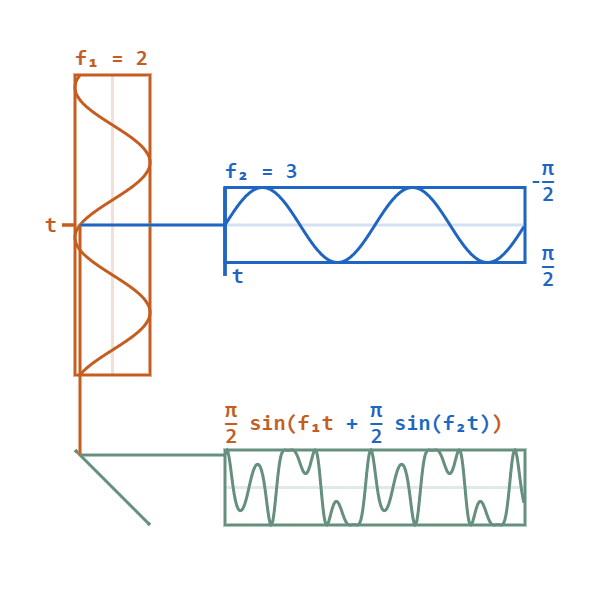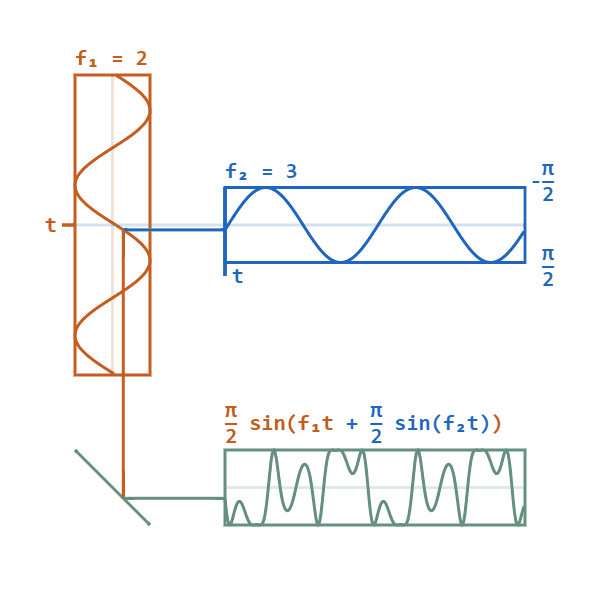
基带为蓝色信号,载波为橙色信号,绿色为PM已调信号
1.3.1 数学形式
相位调制与基带信号成比例地改变复包络的相位角,如果 m(t) 是要传输的基带信号,载波信号 c(t) 为:
c(t) = A_c \sin (\omega_c t + \phi_c)于是,PM调制后的信号为:
y(t) = A_c \sin (\omega_c t + m(t) + \phi_c)非常好理解的数学表达式( ̄▽ ̄)", 在某一时刻,基带信号的幅度越大,载波的相移就越大,但这同样可以被视作 载波的频率改变,所以PM在某种程度上可以被视作FM的一种特殊情况,其中载波频率调制由相位调制的时间导数给出,也就是如下形式:
m(t) = \cos(\omega_c t + h\omega_m(t))PM的频谱结构表明有2个需要重点考虑的信号区域:
- 对于小幅度信号,PM非常类似于AM,但不幸的是PM的基带带宽增加了一倍,导致效率非常低。
- 对于单频大正弦信号,PM非常类似于FM,其带宽约为:
2(h+1)f_M,f_M=\omega_m/2\pi,h是调制指数,这也被称为PM的卡森带宽法则。。
1.3.2 调制指数
和其他信号的调制指数一样,这个量表示调制变量在其未调制时的水平附近的变化的程度,PM的调制指数于载波信号的相位变化相关:
h = \Delta \theta\Delta \theta 是最大相位变化量。
1.3.3 PM的性质
- PM的传送功率具有恒定性,不难想象。
- PM的调制过程的非线性性质
PM并不满足叠加性原理,此性质让PM的频谱分析与噪声分析变得非常复杂,但也因此,PM具有优异的抗噪声性能~ - 零相交的不规律性
零相交(zero-crossing)是指,在时间轴上,波的幅度由正变成负或由负变成正的瞬间。而一个PM波的零相交并没有规律性存在。事实上,PM波的零相交不规律性,是因为调制过程的非线性性质所致。 - 信息波形难以形象化
对于调幅,只要调制百分比小于百分之百,便可以将调制波的包络视为信息波。但是,PM的波形非常抽象...这也是因为第二条性质所致。 - 可通过增加传输带宽来换取更好的噪声性能表现
和AM相比,相位调制一个非常好的优点是 它可以改善噪声性能。因为对于相加性噪声,调制相位比调制幅度受噪声的影响要小很多。
但是,PM噪声性能的改善是通过牺牲传输带宽来实现的。相比之下,AM不可能有这样的机会~
1.4 AM/FM/PM应用与对比(多图)
AM与FM在无线电广播中应用很普遍,例如我们耳熟能详的 86.6MHz FM广播,衬衫的价格是9磅15便士。
AM与FM的频率划分各地略有不同。在中国,调幅(AM)广播频段为 525kHz-1605kHz频率段,这个频段被称为 中波。调频(FM)广播频段为 88MHz-108MHz,我们一般听的车载电台都是FM。市面上常见的收音机多为FM收音机,而AM收音机已经比较少了。但是如果您也是xidian学生的话,你的电装实习项目就是做一台纯模拟的AM收音机:)
| 调制方式 | 角度调制 | 噪声性能与应用 | 载波特征 | 成本与复杂度 |
|---|---|---|---|---|
| AM | No | 很差,应用场景较少 | 载波频率不变,幅度跟随基带变化 | 可低可高 |
| FM | Yes | 很好,是高频、高保真无线电传输的标准 | 载波幅度不变,频率跟随基带变化 | 相对较高 |
| PM | Yes | 很好,在数字传输编码方案中应用广泛 | 载波幅度不变,相位跟随基带变化 | 相对较高 |
然后我还请来了两位老师,有请示波器和信号源——
1.4.1 AM的实际波形与频谱
原谅我的马虎与懒惰,录制波形的时候忘了记下参数了...
AM调制波形
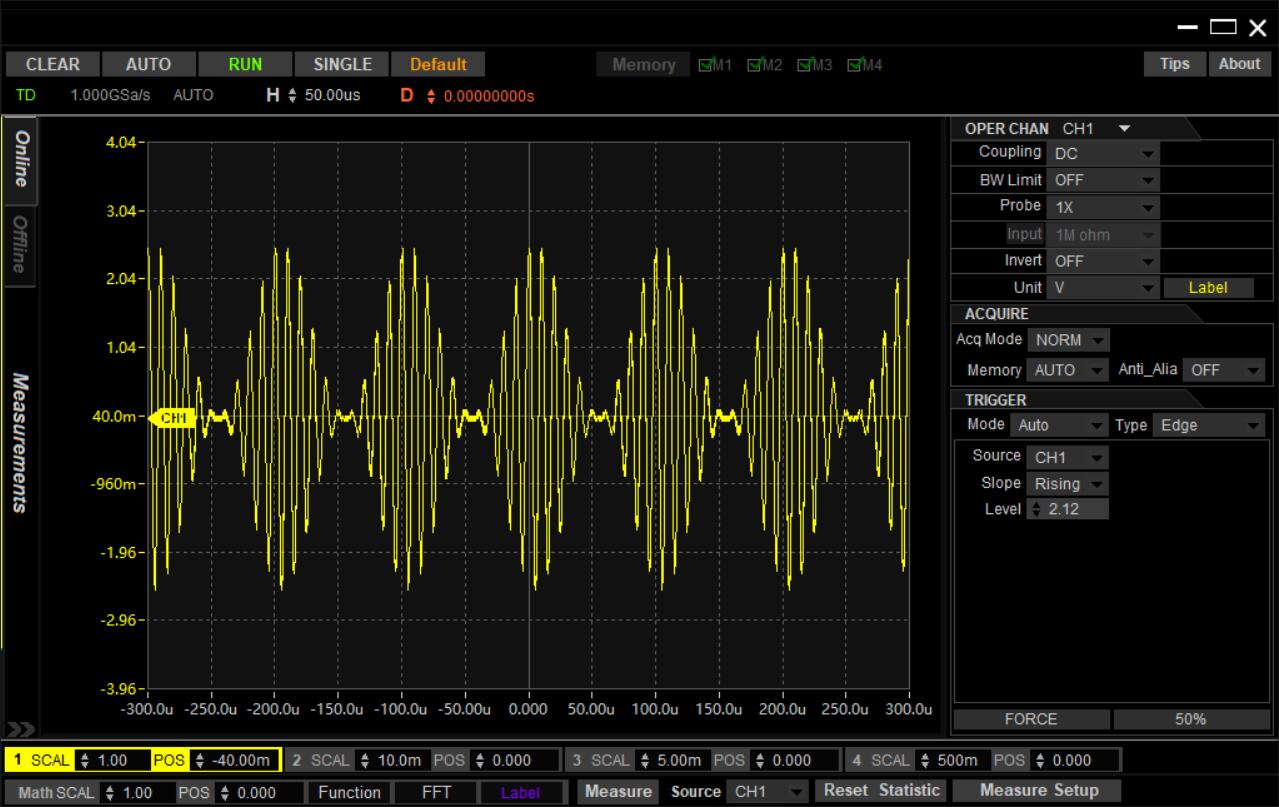
这是标准AM信号的频谱结构,由于我手里没有频谱仪,只能用示波器的FFT功能凑合看一下...
适当调整和加窗之和还是可以看出大致形状的,标准AM调制的频谱结构是一个基波加2个边带——
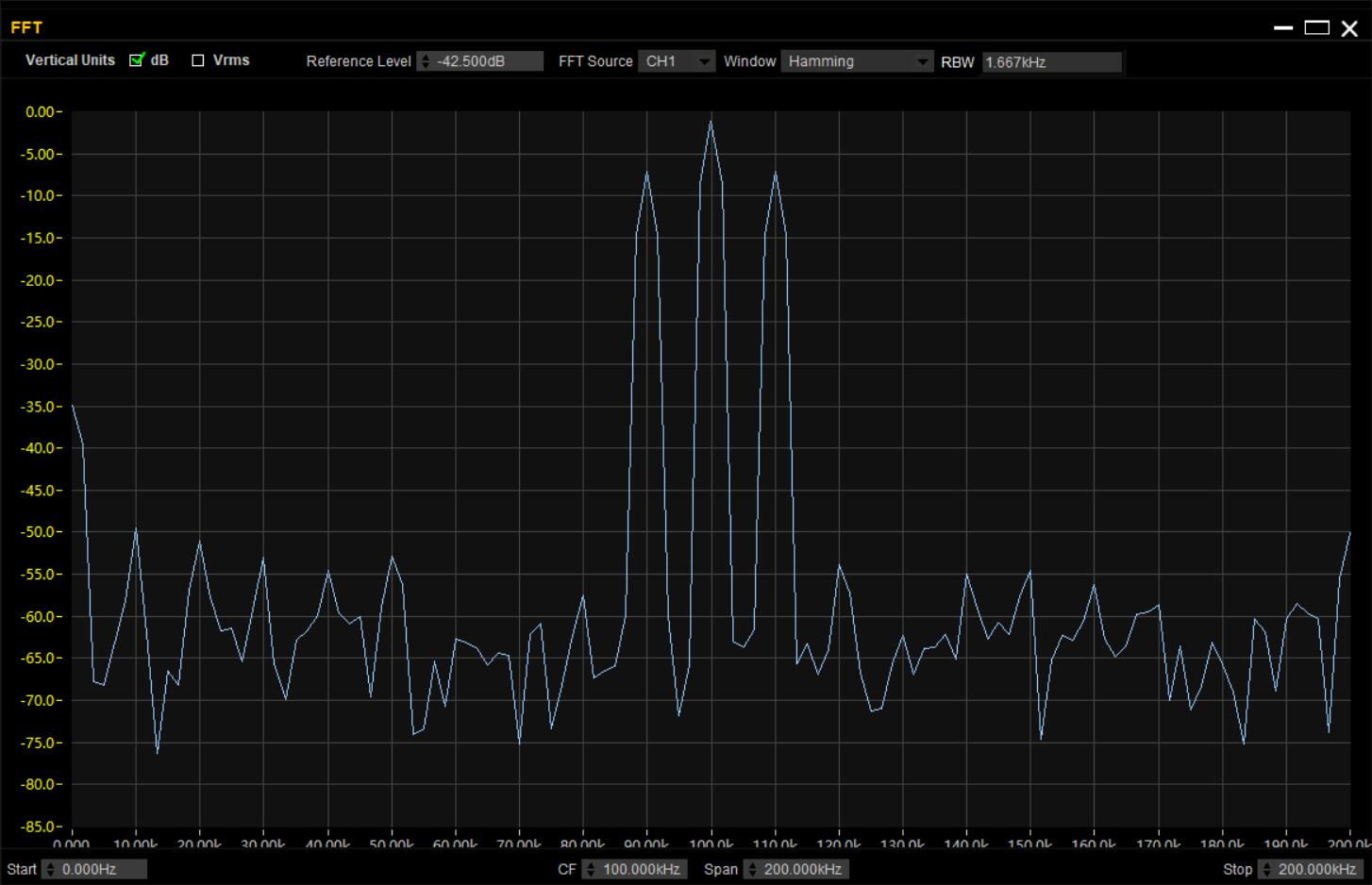
然后我们打开信号源调制的 载波抑制 功能,将标准AM已调信号的基波抑制掉,频谱就变成了这样~
基波不见辣!
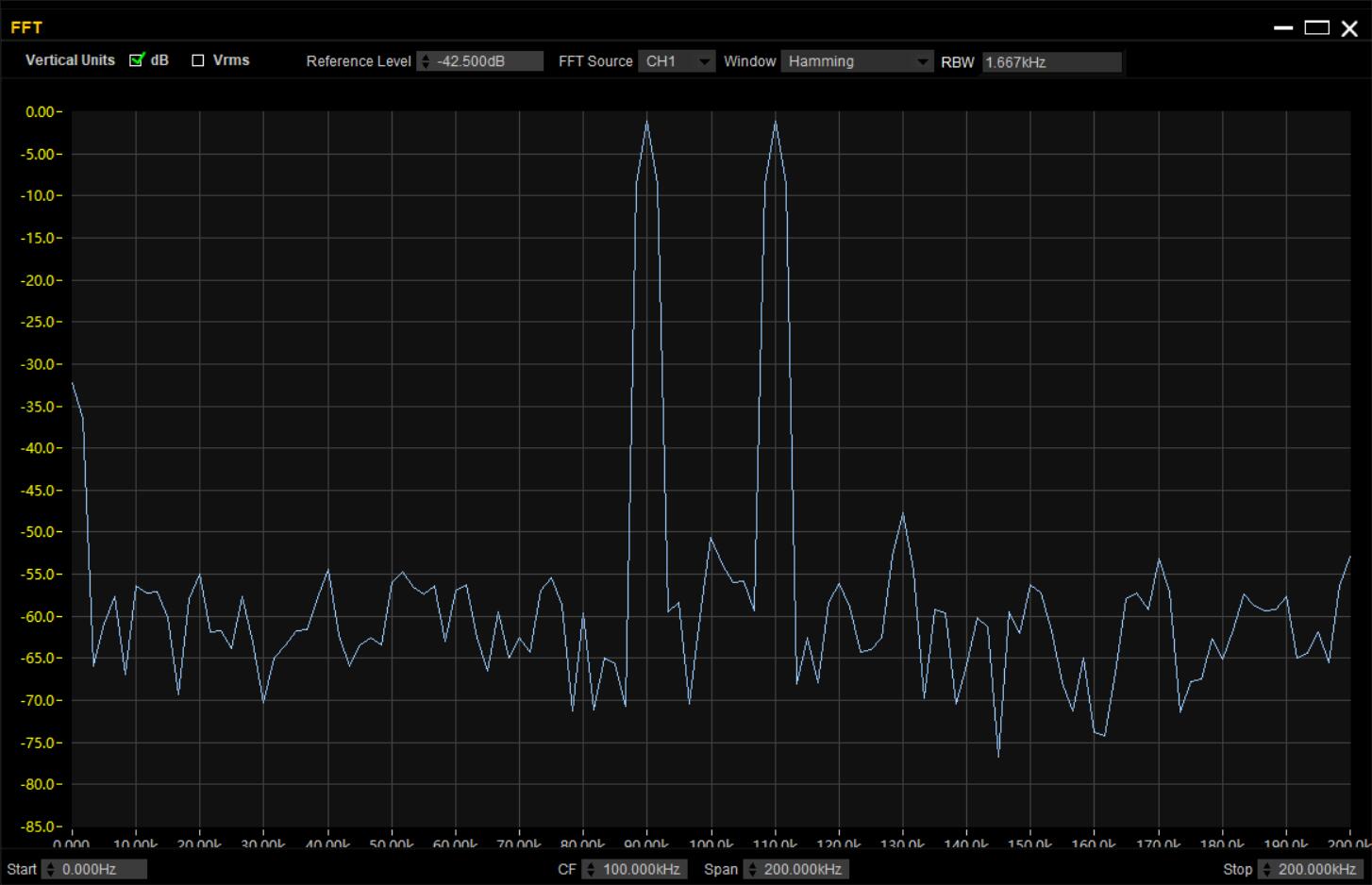
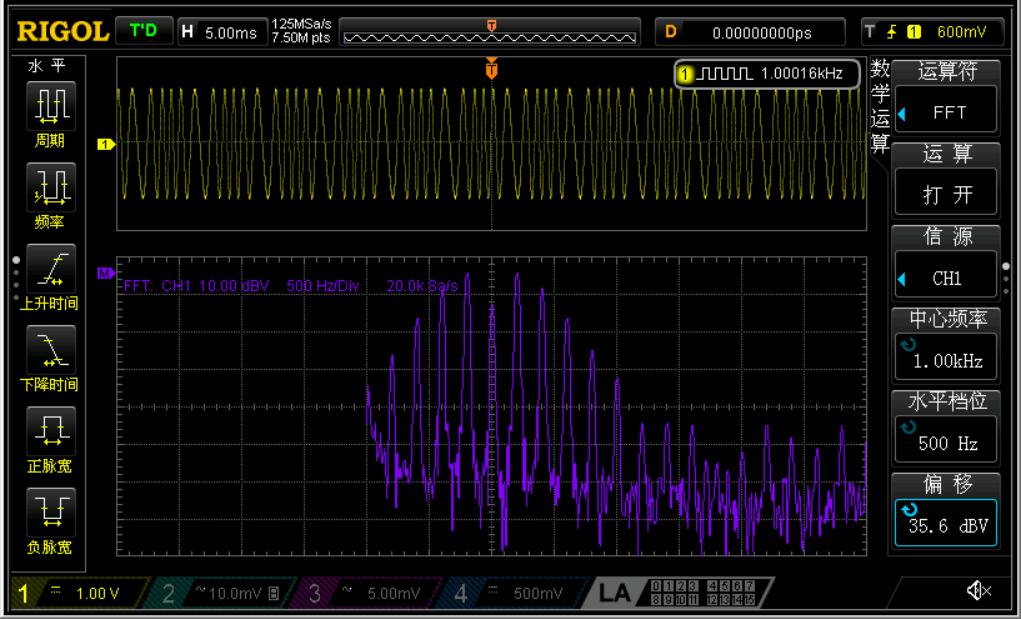
1.4.2 FM的实际波形与频谱
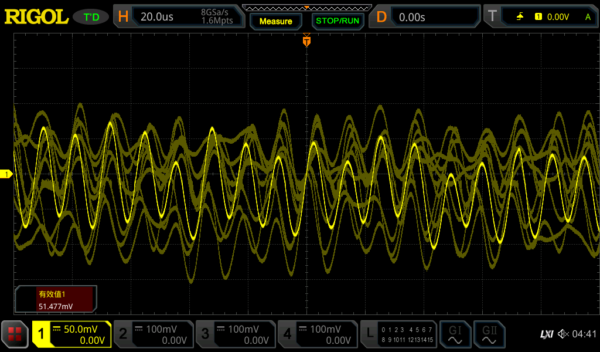
这里由于RIGOL的上位机实在效果不好,我就直接导出示波器截图了...可以看出已调信号的波形一会儿紧凑一会儿稀疏,说明其频率在连续变化。
可以大致看出FM频谱的形状,以及粗略估计一下卡森带宽。当然最好还是拿频谱仪看咯。。可惜俺没有,太穷了。。
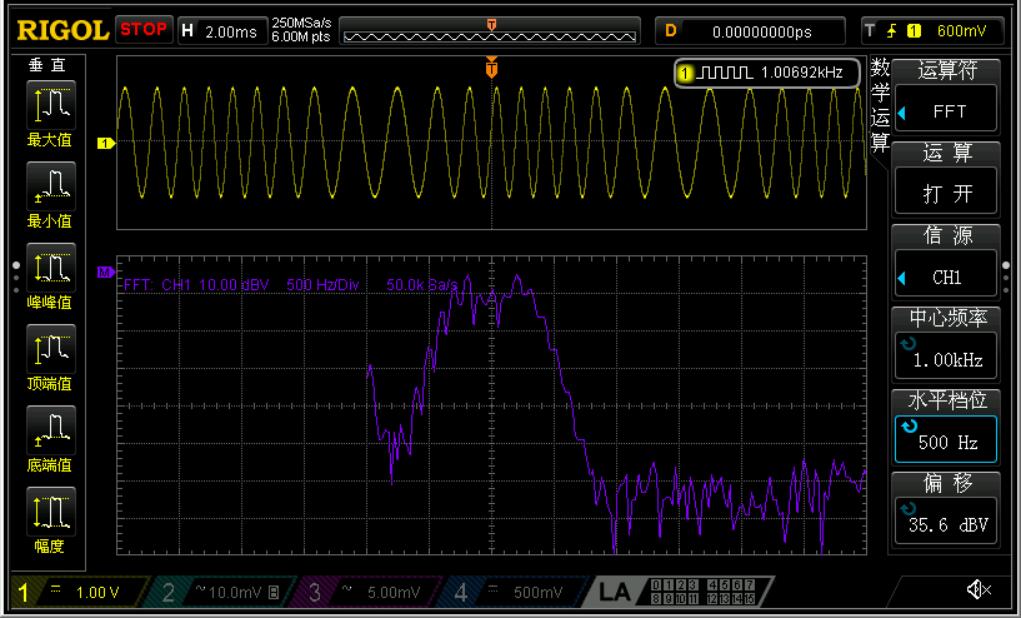
1.4.3 PM的实际波形与频谱
又是一张辣眼睛的截图。这是PM的波形与频谱结构,可以看出相位变化吗?不难发现,PM的波形与FM某种程度上类似,因为它们同属于角度调制~
PM的频谱,因为这台示波器的FFT深度不够,RBW太大了可能有些峰压根没分辨出来..所以凑合看看就行233
3种模拟调制都港完了,我们马上开始进入数字时代!
二.数字调制
之前我们讲的都是模拟域中的调制方式,它们在早期的无线电通讯技术中发挥了重要的作用(比如二战)。随着电子和计算机技术的发展,人们传输的信息量越来越大、通信速率越来越高,传统的模拟调制已经无法满足高数据率通讯的需求了,于是工程师和科学家们利用新开发的技术、器件与芯片,发展了数字通信技术。
在这里我们只介绍基础数字调制,也就是对应于传统模拟调制的 ASK、FSK、PSK。高阶调制在下一章港:D (也可能是下一篇文章😂,具体看鸽子鸽不鸽)
2.0 数字调制与模拟调制的区别
数字调制与模拟调制最重要的区别就是 —— 基带信号。模拟调制的基带信号是模拟信号,数字调制的基带信号是数字信号,当然,在这里我们讨论的前提是 载波为模拟信号。
2.1 ASK(Amtitude-Shift Keying)
ASK中文名叫 幅度偏移调制,又称 幅移键控、幅度键移。ASK是通过载波的幅度变化来表示数字基带信号的,当基带信号为0时,令载波的幅度为A0;当基带信号为1时,令载波的幅度为A1。而A0和A1由我们决定,一般可将A0直接设置为0,A1设置为载波自身的幅度值即可。像下面这样:

是不是非常简单易懂~
我们再回头看看与ASK对应的AM调制:

可以看出,关键的区别在于 基带信号。
这里我们就不去扣ASK的数学特征了,其实跟AM很接近,就是把基带信号换成了数字形式而已。
2.1.1 ASK实现
你可能会好奇,为什么ASK的名称里有 键控 这一词?这当然是跟它的实现方式相关的~
我们有好几种方式来实现ASK调制:
- 模拟开关
- 压控增益放大器
继电器(划去)(开玩笑的,继电器打咩打咩。)- 在数字域中实现
比如说,我将基带信号直接加到模拟开关的控制脚上,当基带为高电平时,模拟开关导通至A通道,A通道接上了载波信号,这时输出就是一段载波信号的片段;当基带为低电平时,模拟开关导通至B通道,B通道接地,这时输出就是一段低电平。(是不是很像按键...)
这里(1和0的情况)对载波信号源也没有什么严苛的要求,它只需要输出一个幅度恒定、频率基本不变的信号就可。略微频移不会影响ASK的接收判决过程,影响该过程的是传输信道和接收机中存在的噪声(当然还有其他诸如失真、传播条件等因素)。
当然,也可以让已调信号为0的那一段不为0。我用信号源输出了一个这样的ASK信号(上),以及它的频谱结构(下):
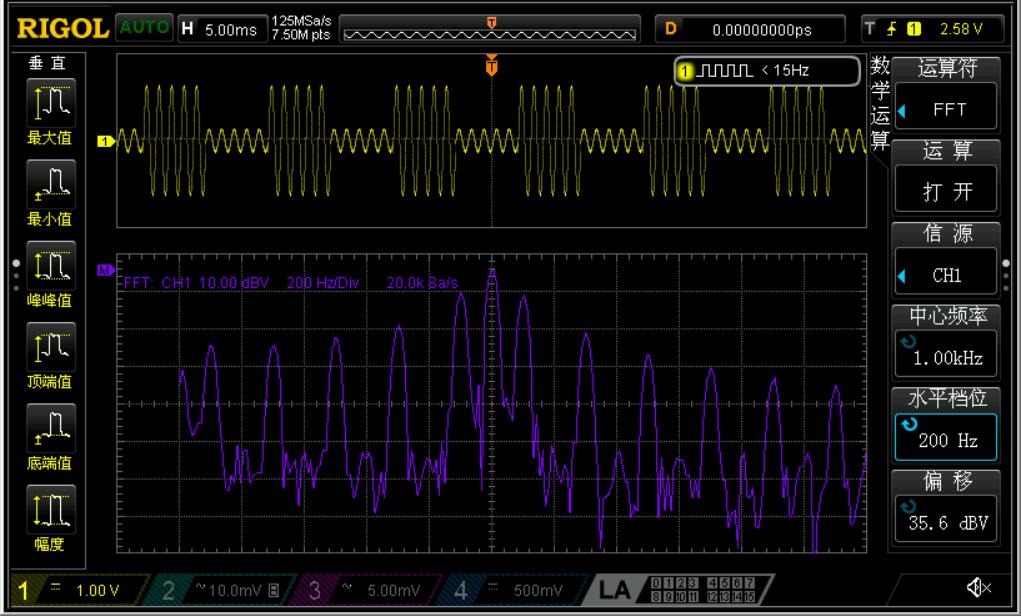
为什么会有这样的频谱结构呢?ASK调制在数学上其实就是一个方波与正弦载波时域相乘,于是在频域中2信号卷积,于是得到了周期延拓的方波频谱。(哦,还有直流分量)
2.2 FSK(Frequency-Shift Keying)
频率偏移调制,又称频率键移(FSK),是一种利用频率差异的信号来传送基带信号的调制方式,和FM类似,不过FM的频率变化是 连续的,而FSK则是具有固定频率差异的一系列离散频率值。
最简单的也是最常见的FSK为 二进制FSK(Binary FSK, 简写BFSK或2FSK)。BFSK利用2个离散的频率值分别代表不同的二进制信号(0和1),更高进制的FSK还有四进制FSK(QFSK)等。
下图所示为一个BFSK的调制示意图。载波为一单频正弦波,当基带信号为1时,输出频率比载波略高一些;当基带信号为0时,输出频率比载波略低一些。而这个频率差异是上下相等的。

2.2.1 FSK实现
不知你注意到没有,上面的BFSK波形中,已调信号的频率过渡非常地 平滑,其实这被称为 相位连续。如果相位不连续的话,你可能会在频率过渡点看到间断点,体现在波形上就是尖峰。
我们如果使用最直接的方法来实现FSK:搞2个不同频率的正弦信号源,然后用基带信号控制模拟开关来控制2个信号的通断,就像我们在ASK上做的那样——那么我们几乎不可能保证频率过渡点的相位连续,因为很难去控制2个相互独立的信号源的相位实时同步。
那么相位连续的FSK怎么实现呢?通常我们是在数字域中实现这一过程,即根据基带信号在处理器上实时调制(计算出波表),然后利用高速DAC输出已调信号。
另一种方法是使用 DDS 器件。我们之前的文章 利用STM32的片上DAC实现DDS(数字频率合成) 对DDS做了详细的介绍。有的DDS具有2个频率寄存器,使用基带信号去控制使用哪一个频率寄存器,即可实现相位连续的BFSK调制。
同样的,附上一张信号源输出的FSK信号波形与频谱图:
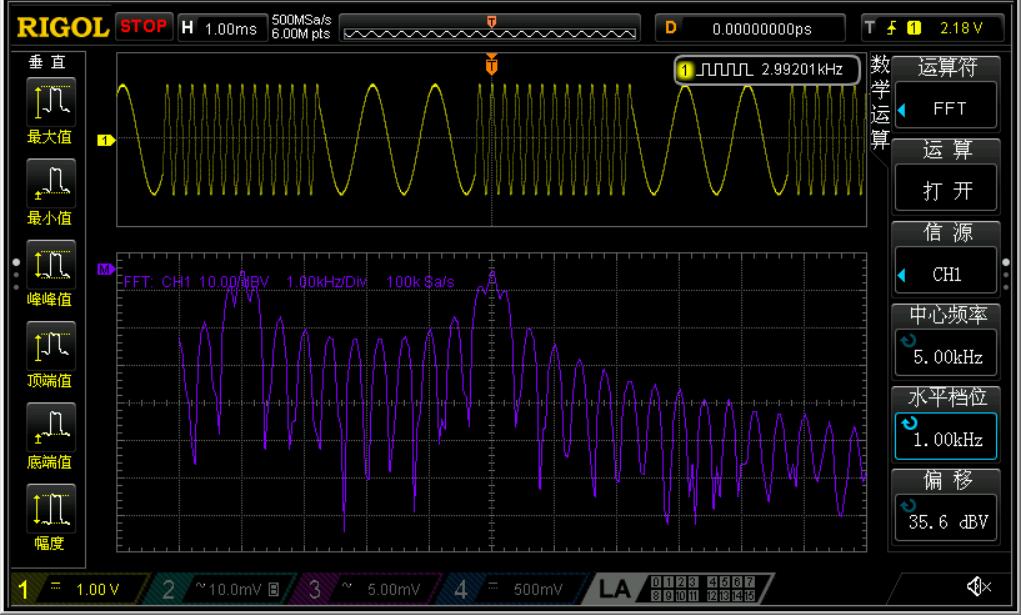
嗯,我怀疑这个频谱的频率分辨率不够,有些峰混一块了。
2.3 PSK(Phase-Shift Keying)
相位偏移调制,又称相位键移(PSK)利用相位差异的信号来传送基带信号。PSK在无线网络、蓝牙、RFID等无线通讯技术中应用广泛。
PSK又可称为 M-PSK 或 MPSK,M代表传送信号的 符号(symbol)种类。符号种类越多(M越大),传送的bits数越多,通信速率越高。比如说二进制PSK的M=2,一般称为BPSK或2PSK。相应的还有4进制(QPSK)、8PSK、16PSK等。但M-PSK会因M的提升而使得误码率上升,M大于16之后误码率(BER)就有点大到无法接受的程度了,所以16之后都由另一种高阶调制——QAM来执行调制工作。
误码率(Bit error Rate, BER)是指单位时间内接收到的错误bit的数量。
举一个例子,假设传输的比特串行为:
0 1 1 0 0 0 1 0 1 1
而接收到的比特串行为:
0 0 1 0 1 0 1 0 0 1,
在本例中,差错比特的数量为3。误码率为差错比特数3除以传输的比特数10,也就是0.3或者30%。
M-PSK的误码率与信噪比的关系,可以看出在相同信噪比条件下,多符号种类会导致更高的误码率(BER)

由于ASK和FSK的数学形式与前述模拟调制类似,所以就没有详细说明。但到了PSK这儿,还是说说为好~
2.3.1 数学形式
以二进制PSK(BPSK)为例,BPSK的通用形式遵循以下公式:
s_n(t) = \sqrt{2E_b \over T_b} \cos(2\pi ft + \pi (1-n)) \cdots (n = 0,1)这样,BPSK的信号有2种状态,分别是相位为0和相位为 \pi 两种,也就是:
s_n(t) = \sqrt{2E_b \over T_b} \cos(2\pi ft + \pi) = -\sqrt{2E_b \over T_b} \cos(2\pi ft), \cdots binary "0" \\
s_n(t) = \sqrt{2E_b \over T_b} \cos(2\pi ft), \cdots binary "1"2.3.2 星座图(Constellation diagram)
数字通信领域中,经常将调制信号在 复平面 上表示,以直观的表示信号以及信号之间的关系。这种图示就是星座图。它将信号显示为符号采样时刻复平面中的二维xy平面散射图,从水平轴逆时针旋转,测量到的点的角度表示载波相对于参考相位的相移,测量到的点到坐标原点的距离表示信号幅度或功率。
比如下面这个就是BPSK的星座图,它有2个点,分别代表基带为1时的信号状态和基带为0时的信号状态。

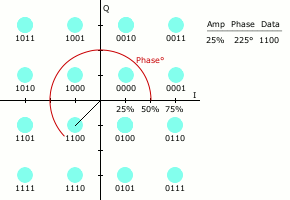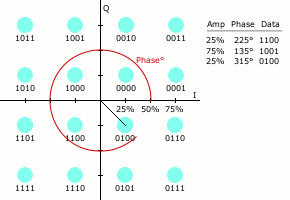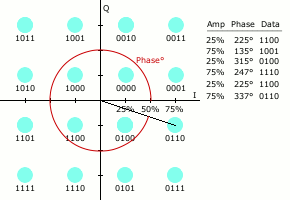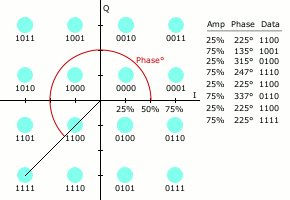
而更高阶的调制,比如QPSK就有4种符号,对应的星座图就有4个状态。比如下面这张图,请注意,这张图中的符号编号并非是简单的二进制编码,而是被称为 格雷码(Gray Code) 的编码格式。

星座点数越多,每个符号能传输的信息量就越大。但是,如果在星座图的平均能量保持不变的情况下增加星座点,会使星座点之间的距离变小,进而导致误码率上升。因此高阶星座图的可靠性比低阶要差。下图为16QAM (QAM既对幅度调制,也对相位调制) 的星座图动态演示,它具有16种符号,传输能力更强,但是也因此每个符号之间的间距小了很多。
2.3.3 I/Q
如果你想更深入地了解数字通信系统,那么I/Q调制是必不可少的内容。当然这个I/Q不是描述智商那个IQ。
我们预计会在后续文章中详细介绍I/Q调制,你也可以看看这里学习一下: I/Q Data for Dummies
2.3.4 Waveforms
差点忘了附上PSK的波形图了~应该可以看到相位突变点吧?
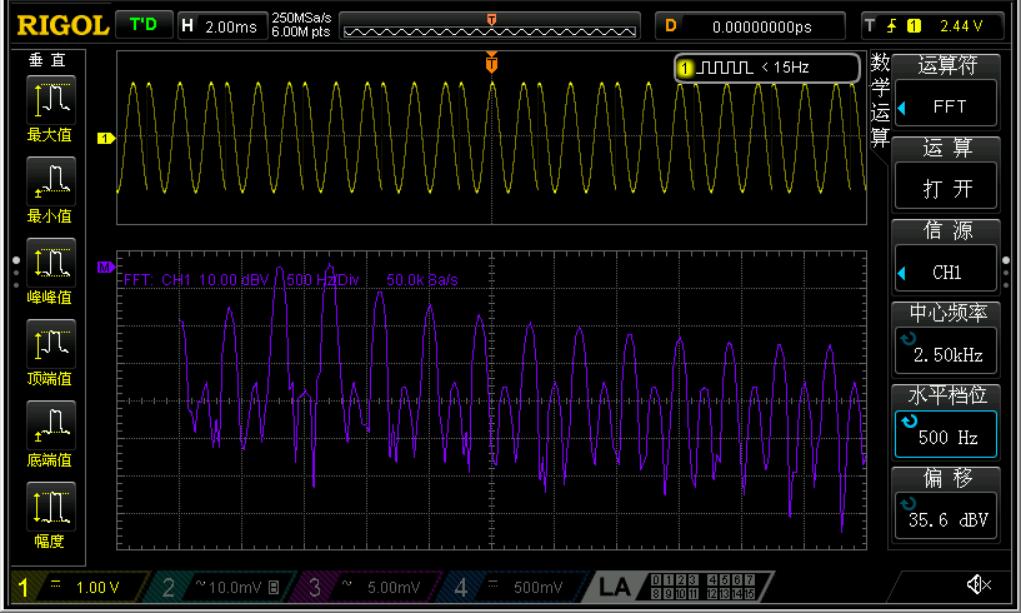
三.特殊信号
为什么要讲这个呢...因为这些特殊形式的信号与我们的通讯领域息息相关,尤其是雷达。有必要康康)
3.1 Chirp(啁啾)信号
啁啾(Chirp)是指 频率随时间而改变(增加或减少) 的信号。其名称来源于这种信号听起来类似 鸟鸣的啾声。在这里我们只是简单介绍一下。
比如说线性Chirp信号的波形长这样:

线性啁啾的时频谱(👇),显示频率随时间变化为线性,由0至7 kHz,每2.3秒重复。图中,色彩的鲜艳度表示讯号在指定时间和频率所含的能量。
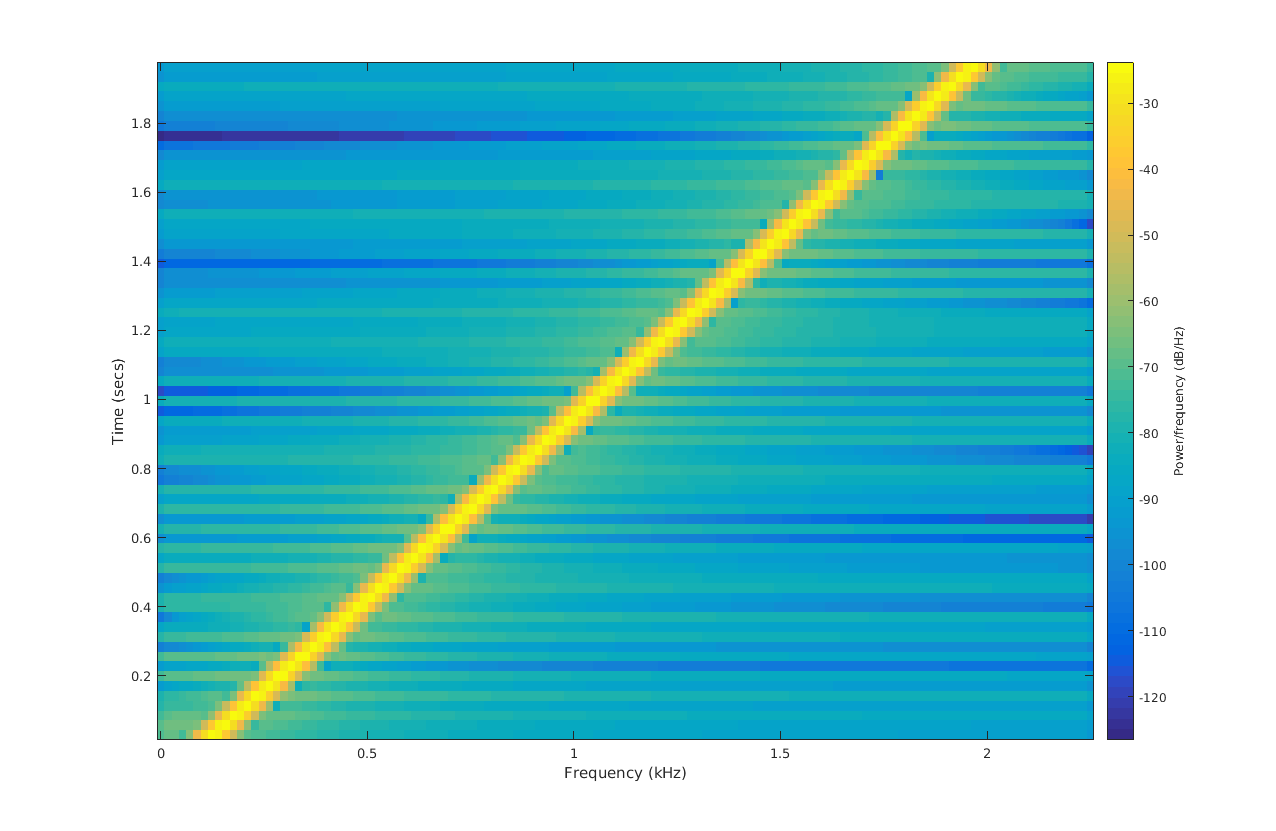
然后还有指数变化的Chirp信号,可以看到它的波形变密集的速度(频率升高)非常快。
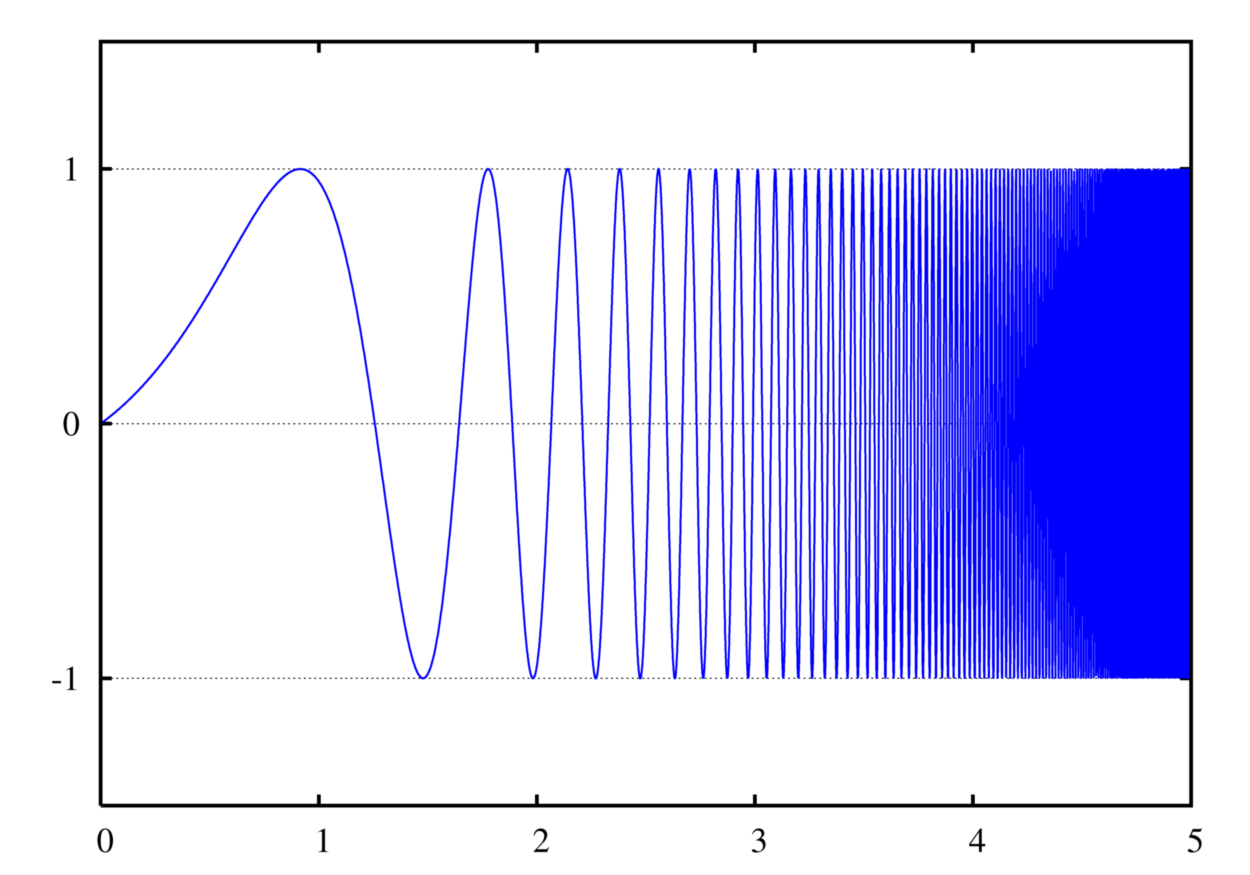
指数啁啾的时频谱(👇),显示频率随时间变化为指数规律。图中,色彩的明暗度表示讯号在指定时间和频率所含的能量。
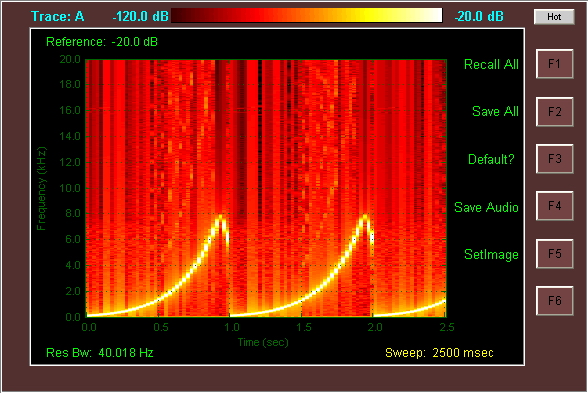
3.1.1 Chirp信号的产生
常见的有3种产生方法:
- 使用一锯齿波控制压控振荡器(VCO),以此来产生频率线性增长的Chirp信号
- 在数字域中合成Chirp信号(在DSP中直接运算出波形数据),然后用DAC直接输出
- 使用DDS器件,直接修改频率控制字(Frequency Tuning Word)
3.1.2 Chirp信号的用途
说到Chirp信号的用途,就不得不提我们之前的雷达信号处理系列了——
Chirp信号由于其跟脉冲信号的相关性(数学上),非常适合用于无线电和声波探测技术中的 脉冲压缩 技术上。所以首先Chirp可用于雷达和声纳上,能够使这些系统测量长距离的同时又保持高时间分辨率。
然后在声学上、医学和波物理学上也有相关的应用。详情请看Wiki~
四.高阶调制
这一章是某只鸽鸽说要写的,但是他还在咕咕咕...
五.推荐学习资料
在写这篇文时,我在网上到处扒拉教程和参考资料,自然也找到了一些非常有趣的、实用的教程,在这里推荐给各位~
PySDR - 利用Python交互式地学习通信原理与软件无线电(SDR)
这个网站的作者也是 GNU Radio Project 的leader之一,非常牛逼...
I/Q Data for Dummies - 利用图形形象地解释什么是I/Q
我觉得这篇文章是能搜到的讲IQ原理讲的最好的一类了。作者本人也非常有意思,计算机网络&安全&机器学习专家...
Matlab Communication Toolbox - 通信工具箱
作为享誉科学界和工业界的科学计算与仿真软件,Matlab也具有一整套与通信有关的仿真工具,这个仿真工具箱几乎能做现在存在的所有通讯相关技术的底层、上层仿真,非常强大。当然,也可以用它搭配Simulink使用,就更nb了。
Think-DSP
这是一个Professor —— Allen Downey 写的一本电子教材,他旨在通过Python及其众多功能强大的库来呈现数字信号处理(DSP)的无限魅力...总之是计算机与EE完美结合的典范~
Reference
- 射频电路基础-邓军,赵建勋-西安电子科技大学出版社
- Modulation-Wiki
- 振幅调变-Wiki
- Amptitude Modulation-Wiki
- AM调制器混频器电路-QA Stack
- 频率调制-Wiki
- Frequency Modulation-Wiki
- 相位调制-Wiki
- Phase Modulation-Wiki
- 长波、中波、短波、微波通讯区别在哪?-湖南无线电管理
- Amtitude-shift Keying-Wiki
- Frequency-shift Keying-Wiki
- Phase-shift Keying-Wiki
- 相位偏移调制-Wiki
- 比特误码率-Wiki
- 星座图-Wiki
- 啁啾信号-Wiki
- Chirp-Wiki
- Constellation diagram-Wiki
- PySDR
- I/Q Data for Dummies
- Think-DSP

![[Bonjour STM32]No.番外-优雅地开发STM32](https://www.emoe.xyz/wp-content/uploads/2020/05/clion-1-logo-600x450.png)
![雷达信号处理-[3]-数字下变频(DDC)](https://www.emoe.xyz/wp-content/uploads/2021/11/1-1-600x184.png)