本文目录

[魔法电路]-电路中的噪声

最近🐟在精密测量的巨坑中打滚，最近在做的 EmoeMetrology项目中，我遇到了疑似关于闪烁噪声的问题，遂作此文，整理一些有关于电路中的噪声的问题，以及消除噪声的方法。多数资料来源于Wiki，以及ADI的技术文档。在文章末尾会贴出链接

噪声定义

噪声（Noise）在电子学中指，信号在传输过程中会受到一些 外在能量所产生信号（如杂散电磁场）的干扰 ，这些能量即噪声。噪声通常会造成信号的失真。其来源除了来自系统外部，亦有可能由接收系统本身产生。噪声的强度通常都是与信号带宽成正比，所以当信号带宽越宽，噪声的干扰也会越大。所以在评估噪声强度或是系统抵抗噪声能力的数据，是以信号强度对噪声强度的比例为依据，此即 信噪比（Signal to Noise Ratio, SNR）。

噪声从来源上分类可分为外部噪声和内部噪声两种。外部噪声主要的来源是:

大气层
外太空
人为噪声

而内部的噪声主要是 热噪声（Thermal Noise）。这种噪声是电阻性元件内部 电子随机移动（电流是宏观效应，即"电子的定向移动"，但在微观下也会存在不遵循这一趋势的部分电子，即为噪声） 所产生的，它的强度和电阻的环境绝对温度成正比。在极低频段下，还有一类不易观察的噪声来源，被称为 1/f 噪声。这类噪声是由半导体工艺所导致的。

噪声的特性与分类

噪声虽作为一个随机信号，仍然具有统计学上的特征属性。功率谱密度（功率的频谱分布）即是噪声的特征之一，从而人们可以通过它来区分不同类型的噪声。在一些噪声扮演着重要角色的研究领域中（例如声学、电子工程和物理），这种噪声分类方法通常会给予不同的功率谱密度一个不同的“色彩”称谓，也就是说不同种类的噪声会被命名为不同的颜色。但是在不同的专业领域间，或许会有不同的术语称谓。

本文主要讲讲电子学领域中的噪声以及对应的颜色。但在这之前我们先了解一下各类不同噪声的统计特性，然后再去关注工程中实际的噪声特性。（不然很容易弄混淆）

1.白噪声

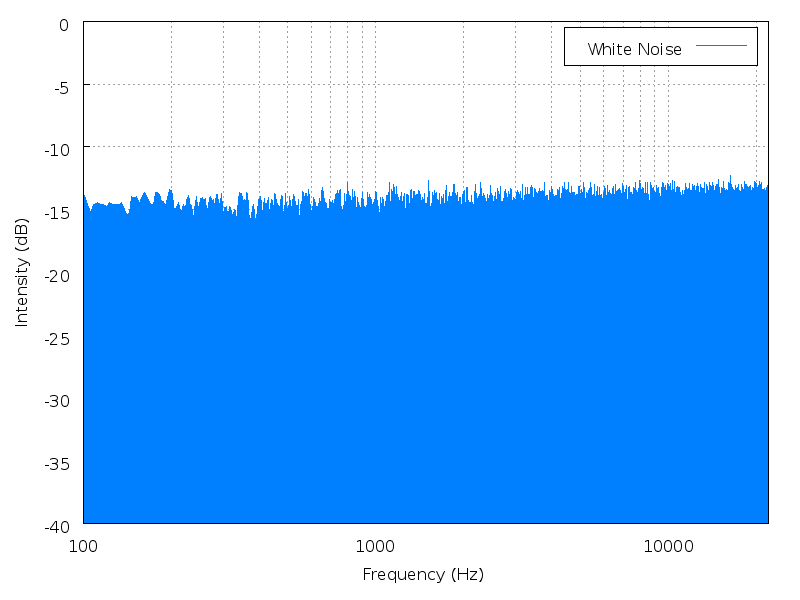
白噪声的名称来自白光，表示在全频域内 单位频域下都分布有相同的能量密度，在线性空间内它具有平坦的频谱。换句话说，一定频域内的白噪声在其中任意给定的带宽内都具有相等的功率（功率谱密度的定义）。例如在40赫兹至60赫兹频域内的白噪声具有和4000赫兹至4020赫兹频域内相同的功率。

需要注意的是，具有无限长带宽的白噪声只是一个理论上的概念，因为在任意频率上都存在相等的功率会导致最终的噪声总功率为无穷大。在实际应用中的白噪声是指在某一特定频域内的谱密度函数是平坦的噪声，一般称之为 带限白噪声（Band-Limited）。

白噪声的频谱，一马平川。

2.闪烁噪声（粉红噪声）

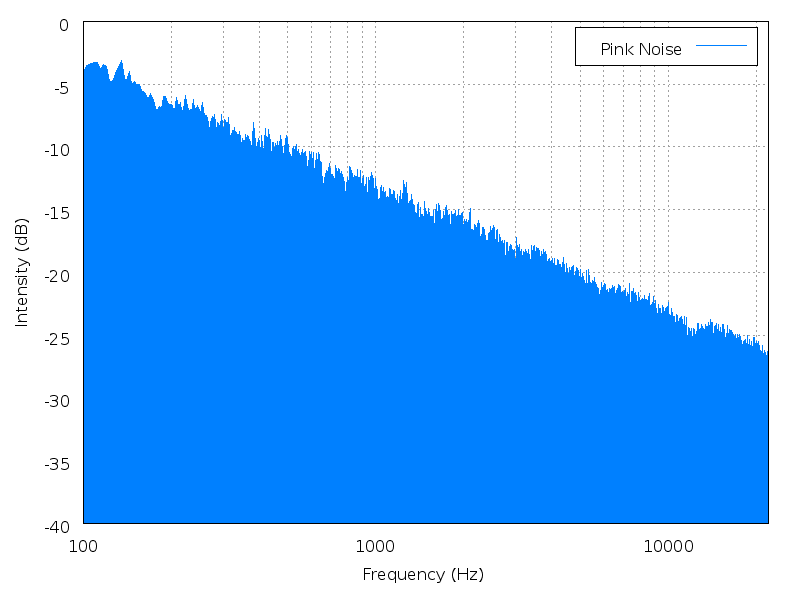
闪烁噪声又称 1/f 噪声、 粉红噪声（粉红噪声的名称源于这种功率谱下的可见光视觉颜色为粉色。），所有的半导体器件在工作时都会有闪烁噪声，它是 由于材料而产生的一种基本现象，在一个特定的噪声拐点下，噪声密度将呈指数增加，而且在低频时将非常大。

更广义的，1/f噪声通常宽泛地指任何一种带有如下所示的功率谱密度的噪声:

 $S(f) \varpropto 1/f^\alpha \\ f为频率，且 0 < \alpha < 2,\alpha一般趋近于1$

1/f噪声的近似功率谱，功率密度以10dB每10倍频程衰减

3.布朗噪声（红噪声&棕色噪声）

布朗噪声又称作棕色噪声或红噪声，是由布朗运动造成的，又称作随机移动噪声。

因此，Brown这个词正确来说是指称发现布朗运动的罗伯特·布朗，而非来自颜色的棕色（真有趣）；至于红噪声的名词则类比于白噪声的由来，因为此种噪声在相当于可见光谱的红光端具有较高的能量强度故得名。

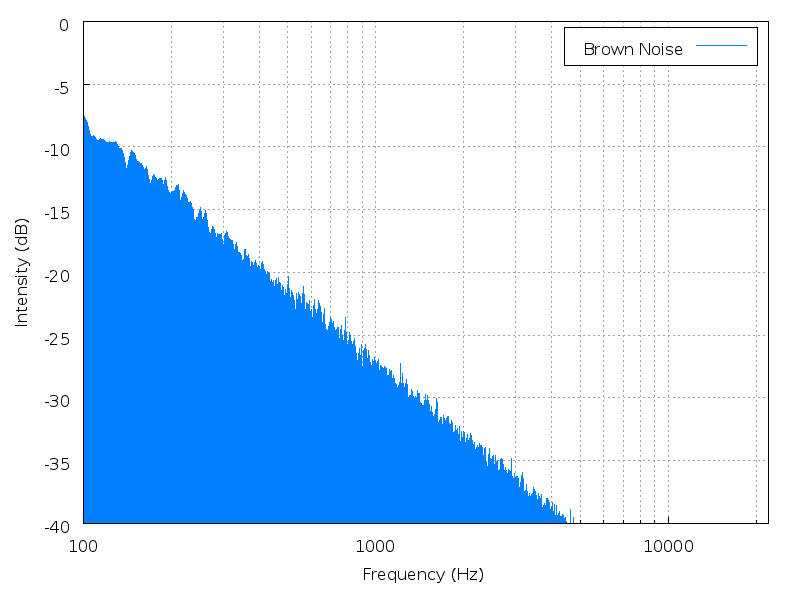
布朗噪声的能量谱密度与其频率的平方成反比，意即该噪声在较低频时有较大的能量， 甚至比粉红噪声还多！。当频率上升两倍时，布朗噪声的能量变衰减6分贝(也就每当频率增加一个数量级，能量变衰减20分贝)。

布朗噪声的频谱图，越往高频衰减得越快（不过这图倒是看不太出来）

还有别的噪声比如蓝噪声、灰噪声等，但我们不讨论太多了，因为我们暂时用不到~

工程中的噪声

上述有色噪声都是从数学和统计学角度出发去研究噪声的特性的，在实际的工程中，会有更加奇怪、更加令人捉摸不透的噪声（毕竟理论终归是理论，总会有欠缺的）。我们来盘点一下工程中的噪声

1.热噪声

热噪声的学名叫 约翰逊-奈奎斯特噪声（Johnson-Nyquist Noise），也可称作约翰逊噪声、奈奎斯特噪声。热噪声是由于热搅动导致导体内部的电荷载体达到平衡状态时的电子噪声，与所施加的电压无关。

一个理想电阻器的热噪声接近白噪声——也就是功率谱密度在整个频谱范围内几乎是不间断的（然而在极高频的时候并不如此）。限定噪声的带宽时，热噪声近似为高斯分布。

热噪声电压与功率

单边功率谱密度（或电压变化（均方）带宽每Hz）由下式给出:

 $\overline{V_n^2} = 4k_BTR \\ k_B是玻尔兹曼常数 \\ T是电阻的绝对温度 \\ R是电阻值（欧姆）$

比如，一个1k的电阻器在室温以及10kHz带宽下的RMS噪声电压是400nV。
还有一个有用的经验法则——50Ω在室温下及1Hz带宽下对应于1nV的噪声。

2.散粒噪声

散粒噪声是一种实验观测中的读出噪声，当观测中数量有限的携带能量的粒子（例如电路中的电子或光学仪器中的光子） 数量少 到能够引发数据读取中出现可观测到的统计涨落，这种读出的统计涨落被称作散粒噪声。这种噪声在电子学、通信和基础物理领域是相当重要的概念。这种噪声的强度随着平均电流强度或平均光强度增加，但是由于电流强度或光强度的增加会使信号本身的强度增加相对散粒噪声的增加更快，增加电流强度或光强度实际是提升了信噪比。这也就是为什么测量、观测微弱信号是如此困难了。

散粒噪声的本质在于，通过测量到的电流强度或光强度能够给出收集到的电子或光子的平均数量，但无法得知任意时刻实际收集到的电子或光子数量。实际的数量可能会高于、低于或相当于平均的数量，其分布按平均值遵循泊松分布。由于泊松分布在大量粒子数时趋向于正态分布，在大量粒子存在时信号中的散粒噪声会呈现正态分布。散粒噪声的标准差此时等于平均粒子数的平方根，信噪比从而为

 $SNR = {N \over {\sqrt N} } = \sqrt N \\ N是采集到的平均粒子数，N很大时信噪比也会很大。$

因此尤其当测量中采集的粒子数很少时，对散粒噪声的分析就显得非常重要。散粒噪声的更进一步研究需要用到量子物理和数理统计的知识，咱没这能力...润了。。

这就引出了一个很有意思的结论，可以解释摄影中的一个问题。
在正常日光下拍摄和夜景拍摄，使用同样的ISO，夜景的噪点明显地会更高。这就是散粒噪声的一种体现咯

3.闪烁噪声（粉红噪声）

1/f 噪声通常是相对于直流电压或电流，因电阻变动而产生的电压或电流变动。就算在没有直流电流流经，电阻器中亦存在因温度变化产生的闪烁噪声。锰镍铜合金则是例外，因为其电阻率的温度系数非常小。在电子电路中，闪烁噪声主要分布在低频，高频噪声大多由白色噪声贡献。然而在震荡器当中，低频噪声会被混合至靠近载波的高频段，产生相位噪声。

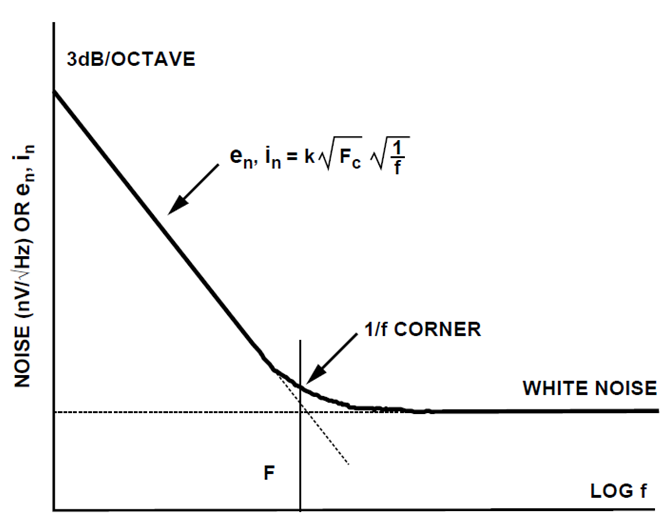
闪烁噪声可由频界频率 Fc 描述其性质，代表由闪烁噪声支配的低频段与由白色噪声支配的高频段之交界处。以常见的半导体元件来说，MOSFET的临界频率相对较高(可高达数GHz)，而JFET与BJT则较低(在2 kHz以下)。此类噪声属于高斯分布，且在时域上具可反转性，产生原因大致上可归因于FET与电阻器中的线性机制，以及BJT中的非线性机制。

功率谱密度中闪烁噪声与热噪声的交界

闪烁噪声也容易出现在碳膜电阻与薄膜电阻，此时它们被视为超越噪声，也就是它们使得整体噪声量总和超越了所有种类电阻器都具有的温度噪声。相反地，绕线电阻则存在最少的闪烁噪声。既然闪烁噪声是基于和直流电流的比较，当电流非常低时，温度噪声（也就是热噪声）将成为电阻器噪声的主要来源，也就是使用绕线电阻并无法在噪声上获得太多改善。

来点具象化的-运算放大器中的噪声

我们就拿电路中最常用的模拟器件——运算放大器为例子，分析一下它的噪声行为。

本节翻译自ADI的技术文章-MT048，我发现Wiki上的那张图就是出自这里（大概）

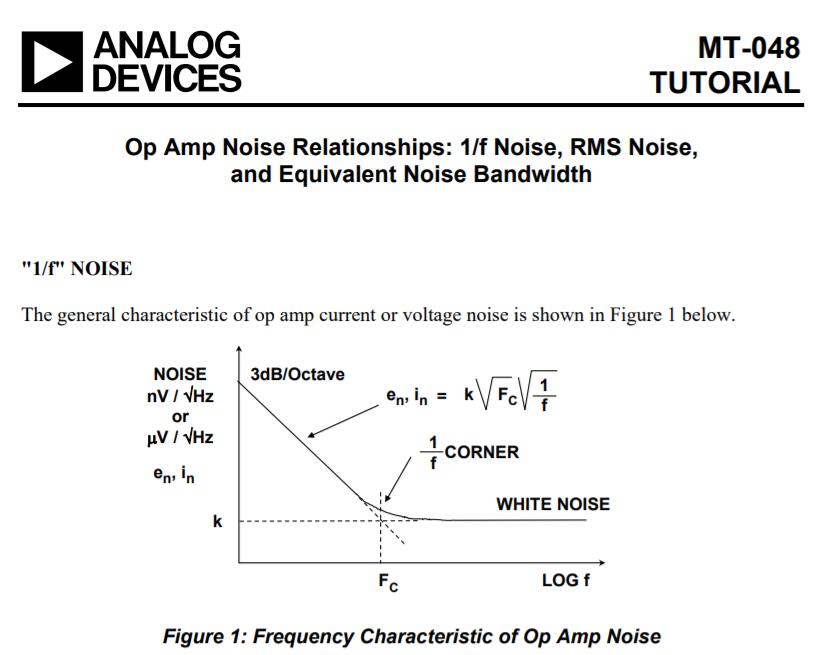
1/f 转折频率

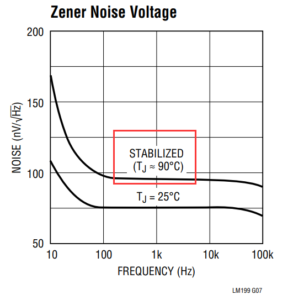
在高频时，运放的噪声趋近于白噪声（因为1/f噪声的特性，频率越高其谱密度越小），这对于绝大多数运放都适用。但是在低频段，噪声功率谱密度以3dB对数上升，就如上图所示。这个区间的噪声谱密度与频率F成反比，所以电压噪声密度是和频率F的平方根成反比的（功率与电压成平方关系）。

因为这个原因，这一段区间内的噪声被称为1/f噪声（ADI说某些老旧教材仍称其为flicker noise，看来这个说法已经过时了。）

这个噪声开始增加的频率点被称为 1/f 转折频率（Fc），很显然的这个值越低越好。对于同一个运放来说，它的电压、电流 1/f转折频率不一定是一样的。一个电流反馈的运放可能有3个1/f转折频率:电压一个，反相输入电流一个、同相输入电流一个。

描述1/f噪声的通用公式（电压、电流均适用）如下:

 $e_n,i_n, = k {\sqrt F_c} {\sqrt{1\over f}} \\ k是白噪声电压或电流的幅度，F_c是 {1\over f} 转折频率$

最好的低频低噪声放大器的 1\f 转折频率约为 1Hz到10Hz，使用JFET的器件和更通用的器件可能会到100Hz。高速运放为了在高频区域的表现，通常会舍弃部分低频性能，可能会导致他们的 1/f 转折频率只有1kHz到2kHz。虽然他们通常用于宽带应用，而且通常是高频下，所以这些低频性能不是那么的重要。但当这些高速器件用在低频时（比如音频），可能会有严重的性能恶化。

RMS噪声计算

噪声谱密度是频率的函数，为了得到 RMS（Root Mean Square，均方根） 噪声，我们需要对噪声功率谱密度在整个带宽上（这个带宽是多少，取决于我们对哪些部分感兴趣，哪些部分可以被忽略）作频率的积分:

 $V_{n, rms} (F_L, F_C) = V_{nw} \sqrt{F_C} \sqrt{ \int_{F_L}^{F_C} {1\over f}df} = \\ v_{nw} \sqrt{F_C} \ln[{F_C\over F_L}] \\ v_{nw}是在'白噪声区间'的电压噪声谱密度 \\ F_L是在 1/f 区间内我们感兴趣的最低频率，F_C是 1/f 转折频率$

下一个我们需要纳入计算范围的区域是从转折频率Fc开始到Fh结束的高频噪声，这个区间内的RMS噪声是:

 $V_{n,rms}(F_C, F_H)=V_{nw} \sqrt{F_H - F_C}$

然后可以把上面2个式子加起来，就能得到从FL到FH频率段内总的RMS噪声:

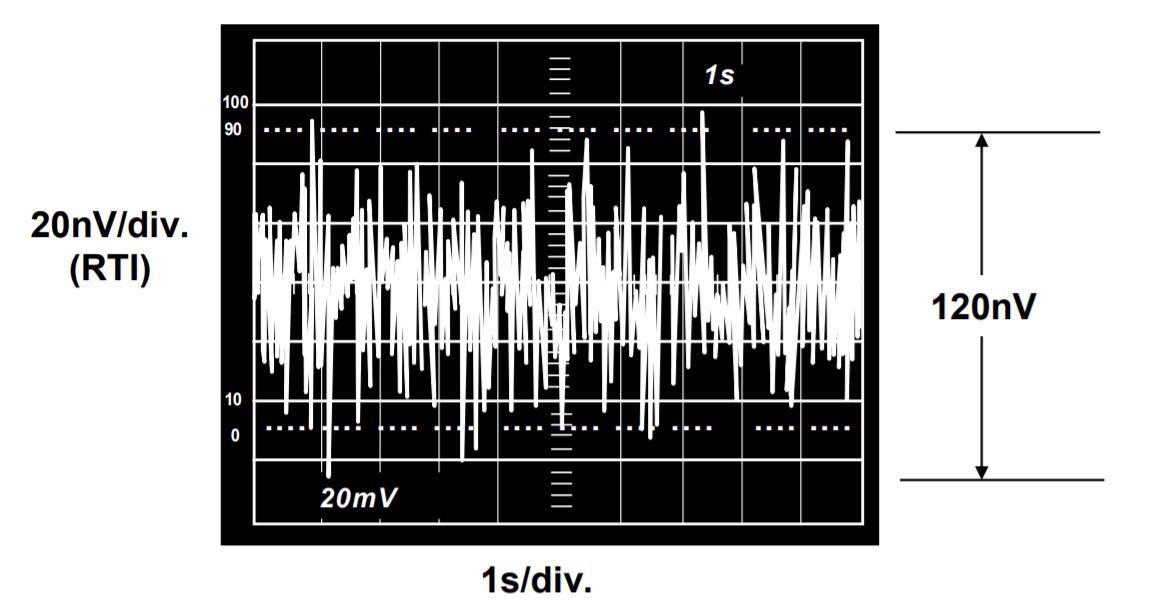
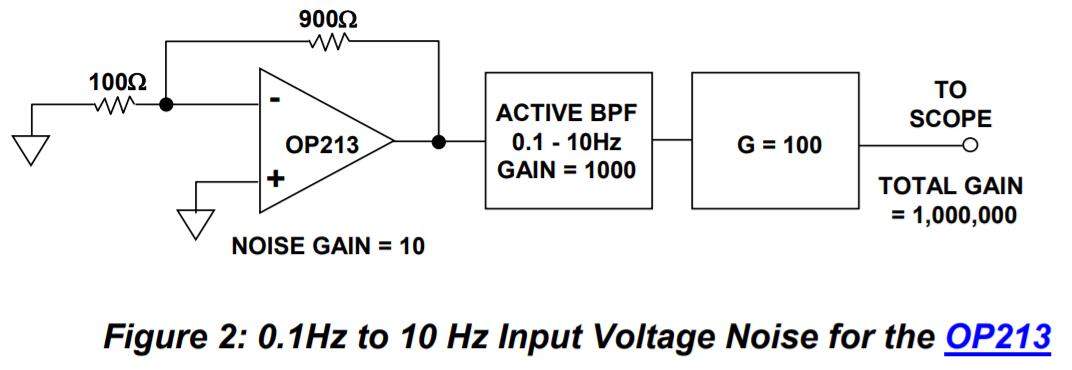
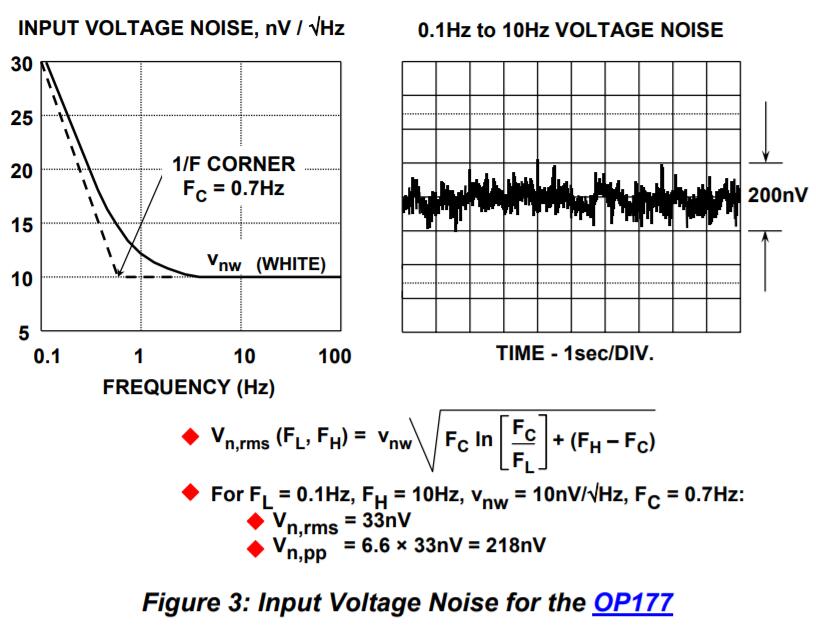
 $V_{n, rms}(F_L, F_H) = V_{nw} \sqrt{F_C \ln [{F_C \over F_H}] + (F_H - F_C)}$

在绝大多数情境下，低频峰峰值噪声通常指 0.1Hz到10Hz 带宽内的噪声。如何测量呢？很简单，用一个0.1Hz到10Hz的带通滤波器，将这一段的噪声提取出来再放大就可以测量了。以下是测试OP213运放的1/f噪声的测试样例。

"所谓的噪声啊，就是噪声吧（雾"

消除1/f噪声的技术

本节参考了ADI的模拟对话文章——如何消除或降低1/f噪声。

可用的一种方法是 斩波（CHOPPING）稳定技术。这是一种降低放大器失调电压的技术，因为1/f噪声是接近直流的低频噪声，所以这种技术也能有效降低1/f噪声。

斩波稳定的工作原理如下: 对输入级的信号进行交替或斩波，然后再对输出级的信号进行斩波，这相当于利用正弦波进行调制。（是不是有点眼熟？像不像之前我发的另一篇文章 锁定放大器？）

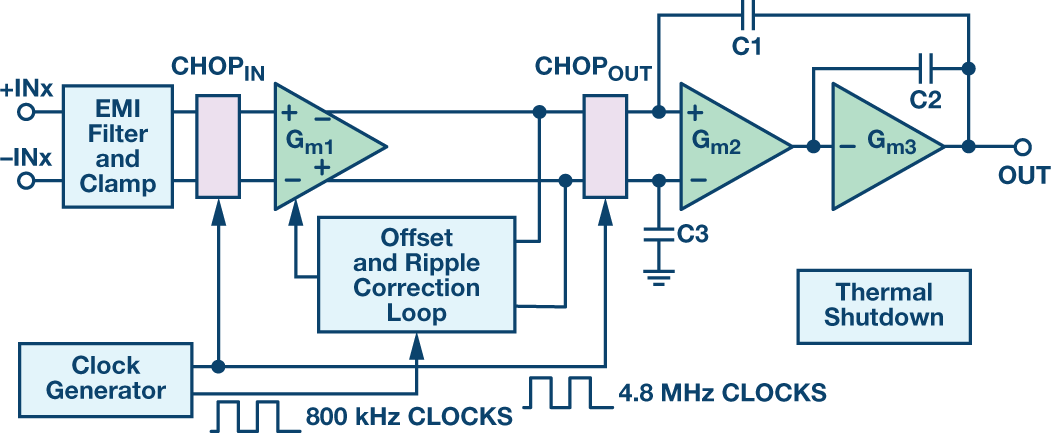
参考上面的ADA4522架构框图，输入信号在CHOP-IN级调制到斩波频率，在CHOP-OUT级，输入信号同步解调回到原始频率，同时放大器输入级的失调和1/f噪声会被调制到斩波频率。除了降低初始失调电压之外，失调相对于共模电压的变化也会缩小，从而获得非常好的直流线性度和高共模抑制比（CMRR）。斩波还会降低失调电压温漂。因此采用斩波技术的放大器常被称为 零漂移（Zero-Offset）放大器 。

但需要注意一点，这种放大器 仅仅消除了放大器自身的 1/f 噪声，任何其他来源的 1/f 噪声会不受影响地通过。

使用斩波技术的缺点也是显而易见的，它会将开关频率成分引入输出并提高输入偏置电流，在示波器上查看时可以看到放大器输出上的毛刺和纹波，用频谱分析仪查看时可以在噪声频谱密度中看到开关频率相关的噪声尖峰，这些高频能量是在CHOPPING的时候混入信号的。不过ADI也有最新的技术去最大化减小这种开关伪像。就是图中的 Offset and Ripple Correction Loop。不知道内部是怎么实现的

时域中的输出电压噪声

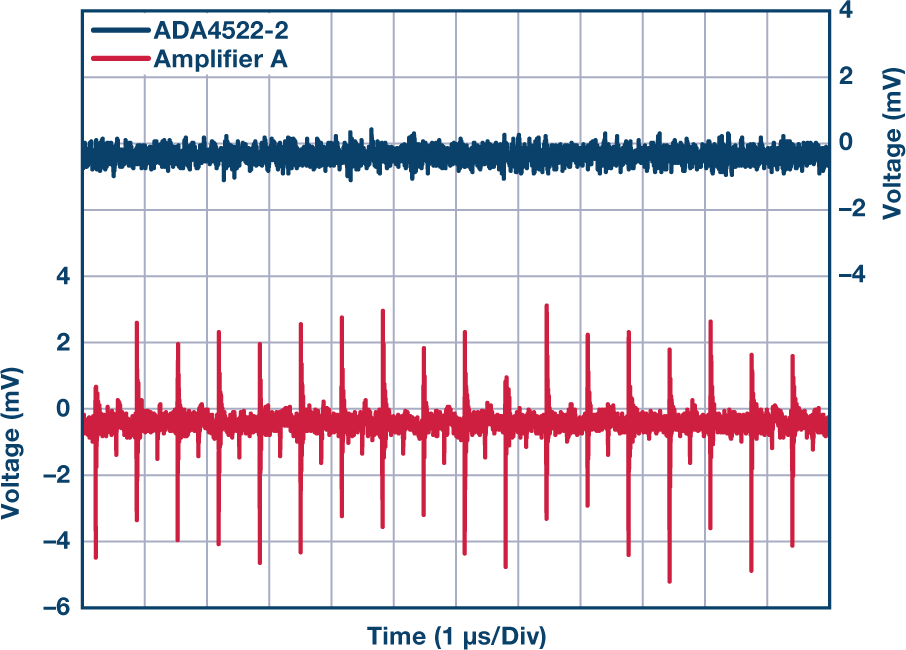
使用方波调制有个缺点，就是方波包含许多谐波，各谐波的噪声会被解调回到最终的输出信号。如果用正弦波调制的话，这种方法受噪声影响要小得多，可以在有大噪声或干扰的情况下还原非常小的信号。这就是我们之前讲过的最正统的锁定放大器用法了~

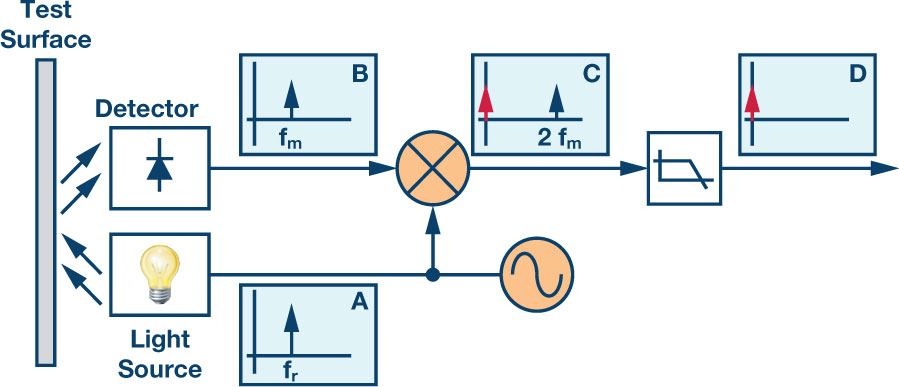
传感器输出正弦波调制信号以控制光源。利用光电检测器电路检测信号。一旦信号通过信号调理级，便可进行解调。利用相同正弦波调制和解调信号。解调使传感器输出回到直流段，但也将信号调理级的1/f噪声移至调制频率。解调既可在模拟域中完成，也可在ADC转换之后的数字域中完成。利用非常窄的低通滤波器（例如0.01 Hz）抑制DC以上的噪声，这样只剩下原始传感器输出，以及极低的残留噪声。这里要求传感器输出恰好在DC，因此正弦波的精度和失真度性能很重要。同样的，此方法 可消除信号调理电路的1/f噪声，但不能消除传感器的1/f噪声。