微观尽头——精密信号测量:Intro

我们一般只会关心身边那些明显的、容易察觉的变化——比如温度变高了几度，车辆的行驶速度变快了几m/s，无所事事的一天又过去了…诸如此类。
但你有关注过一些微不足道的变化吗？比如空气中二氧化碳的浓度具体是多少 ppm（百万分之一） ？你的体重变化了几克？
当然没有吧，因为这些细微的变化超出了人感知的能力，我们自身并不能感受到这些微不足道的变化。

——当然上述多数是一些直观感受，我们只能对其有个大概的把握，并不能精确量化它们。如果在电子测量领域，我们就有许多种手段去量化这些变化。最常用的方法就是利用 传感器（sensor） 去将真实世界中的物理量转化为电信号，并用电子测量电路去对电信号进行处理并分析。

Such as?

比如 电子体重秤。我选了一个烂大街的解决方案来举例子。
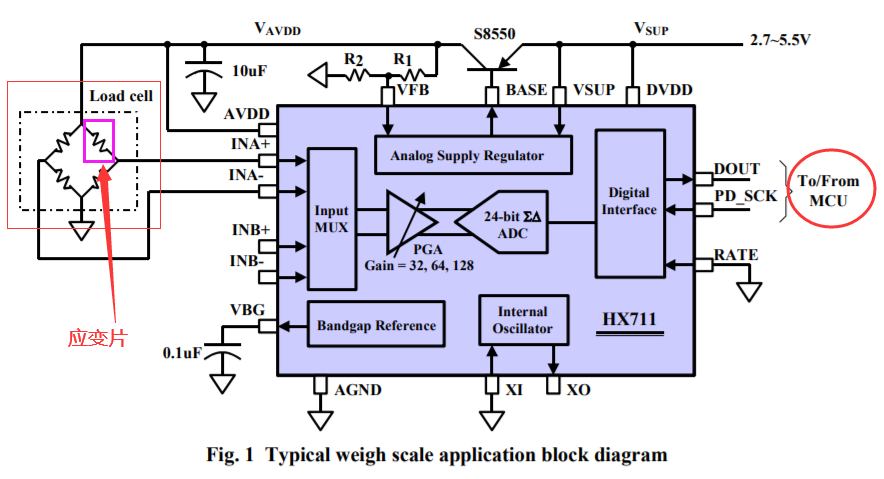
HX711是一片高度定制化的24位ADC,专门用于 桥式电路（Bridge Circuit），也叫惠斯通电桥（Wheatstone bridge） 测量（图中的细线红色方框）。

紫色方框圈出来的是一个 应变片,本质上是一个电阻,它的阻值会随着形变的大小（所受压力）变化，而这个变化是近似线性的。设计一个与其接近匹配的桥式电路，测量中间节点的电压差，就可以实现 压力大小->电压大小 的转换。（你可以画4个电阻拼成一个桥，在上下两端加上电压，测量左右两端的电压，简单分析一下）

HX711

但是这个变化的程度具体有多大呢？有20kg的重物压在其上时和在无形变时，电桥节点处测量到的电压的变化可能只有mV级别。如果直接把这个信号送入测量量程为2V甚至5V的ADC，那么想必测量的精度会相当不理想。来做一个简单的计算:
如果用一个满量程5V、位数为16位的ADC去采集一个5mV的直流电平信号——

 ${5V \over 2^{16}} = 76.3uV \\ {5mV \over 76.3uV} = 65.53 (counts) \\$

这是不考虑噪声和其他误差以及各种各样的干扰的情况下得到的结果。显然直接测量得到的结果基本没有什么参考价值（毕竟我满量程可是65535 counts啊！）

那么很自然的我们需要对这个信号进行调理。（不是tiaojiao）

在上面的HX711框图中，我们可以看到输入选择器（Input MUX）之后有一个 PGA（Programmable Gain Amplifier，可编程增益放大器）。这就是一个简单有效的调理电路。它可以将输入信号放大32倍、64倍、或者128倍之后再送进ADC测量单元去进行测量，5mV的电压经过32、64、128倍放大之后，就变成了160mV、320mV、640mV，这样我们的adc读数就精准多了。。而且这个增益设定是 可编程 的，即可以通过对该芯片内的某个寄存器进行配置从而改变增益，比纯分立元件实现要快捷方便得多，而且整个单元做在一块ic内也保证了信号的质量，同时减少了外界干扰和人为布线引入的未知不良因素（比如骨骼清奇的工程师，可能会做出比较迷惑的设计…）。

最后我们要做的是通过该芯片的数字接口（SPI/IIC等）将测量到的电压数据读出来，并在MCU上作进一步的处理，通过电桥电压与实际压力的数学关系将其转换为重量。当然，整个系统在上电时应该执行 校准（Calibration）操作。你会发现很多电子秤有个功能叫去皮23333。

有意思的坑又增加了！

上述例子中使用的芯片是一个专门为电桥测量设计的高度集成化的 混合信号前端（Mixed Signal Front End）。它包括了激励信号控制、输入选择、信号调理电路、ADC，以及统筹一切的数字接口（当然内部还有带隙基准源，以及内部振荡器）。

tips:通常在应用广泛、工业市场需求量大的领域，半导体公司都会为这种测量需求专门定制混合信号测量前端，以降低系统成本，提高系统集成度。多数数字传感器也都运用了 MEMS（微机电系统） 在芯片内部集成了所有的测量单元以及处理电路，最后直接通过数字接口输出测量到的结果。具体可以去各大半导体公司官网去看看他们的产品线都有哪些~

如果要实现更通用的测量，我们应该自己搭建一套精密信号链。之前🐟买了一个24位ADC模块，经过我的一番测试之后，发现它的有效精度和噪声性能稀烂。。（与模块电路板设计有关）于是我决定自己做一个 地表次精度级 ADC模块，来验证一下其性能。

凿壁偷光

首先嘛，我只是个半吊子学生，还不是一名卓越工程师，没有独立设计精密模拟电路的能力…所以我需要借鉴前辈们的卓越技术与宝贵经验，来让我完成这个设计。

首先我盯上了当年地表最强的DMM——HP 3458A。
在1989年那个只有8051的年代，HP的工程师们就凭借过硬的技术和精湛的技艺，创造了这台8位半的数字万用表，实在是令人叹为观止。在网络上搜集了大量资料，经过几天的剖析，我大致弄懂了一丢丢3458A的构造，这里简单介绍一下。

HP Journal

CNPP同学告诉我说1989年4月的HP Journal专门讲解了HP3458A的核心技术架构，我直接芜湖开冲！

上图是该期Journal的封面图，前面就是我们的主角——大名鼎鼎的3458A，后面是…？
详细翻阅了下面的英文后，得知后面那个大罐子是 Josephson Junction Array，简单来说是 标准电压源。标准电压源的原理是 Josephson Voltage Standard，是用液氦将超导集成电路芯片稳定在4K温度下产生的稳定电压，该电压仅取决于施加的频率和基本物理常数。其背后又是一个诺贝尔物理学奖的故事…

嗯，看着显示屏上的小数点后的位数，一脸满足> <
来到目录，开头的2篇文章将是我们需要重点研读的。

MultiSlope ADC Structure

3458A采用了 多斜率ADC架构（回收标题）来实现高达28位有效分辨率的模拟-数字转换。

The HP 3458A’s ADC uses an enhanced implementation of the same multislope technique to achieve a range of speeds and resolutions never before achieved-from 1B-bit resolution at 100,000 readings per second to 28-bit resolution at six readings per second. In addition to high resolution, the ADC has high integral linearity-deviations are less than 0.1. ppm (parts per million) of input.

3458A采用了改进型的多斜率积分式ADC，可以实现16bit@10KHz 到28bit@6Hz的采样率，并且在整个测量范围内具有极高的线性度（0.1ppm）。要想理解这种高级的改进架构ADC，需要先理解它的前身——双斜率积分式。

双斜率积分

双斜率是一个简单的 积分型ADC算法。以下电路实现了一个比较简单的双斜率积分ADC。

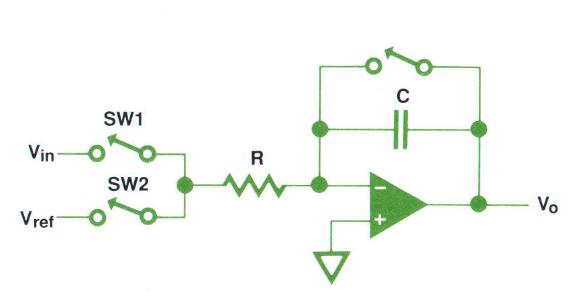
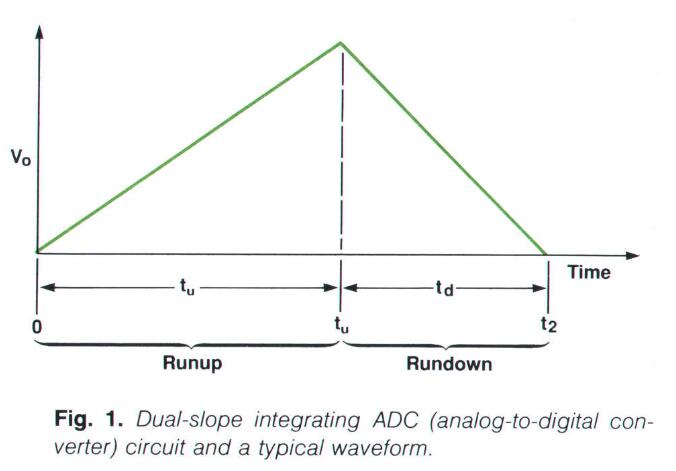
上图是这个算法工作的波形图，先看一眼有个印象。
在双斜率积分算法的初始状态时，电容上的电压为0（电容内无电荷），只需要将电容旁边的开关接通就可以实现。在 t = 0 时刻，断开sw2，接通开关 sw1，未知的输入电压（待测量电压）Vin通过电阻R施加到电容C上，这个充电时间是可控制的，记为tu，这个充电的过程叫做 "runup"。在runup的结束时（将sw1断开时），Vo的值可以用下式表示:

 $V_o(t_u) = -(1/RC)\int_0^{t_u}V_{in}(t)dt$

如果Vin是不随时间变化的（DC）,那么Vo可表达为:

 $V_o(t_u) = -(1/RC)V_{in}t_u$

下一步，将sw1断开，接通sw2，将 与Vin极性相反的Vref 施加到电容C上，这时将启动一个 计数器（counter），当电容上的电压降至0的时候，计数器停止计数。这个过程就叫 "rundown"。当这个过程结束之后，计数器计数的值的大小就可以代表未知输入电压的大小:

 $V_o(t_2) = V_o(t_u) - (1/RC)V_{ref}t_d = 0,$

td就是rundown这个过程所需要的时间，有了这些就可以求解出Vin:

 $V_{in} = -V_{ref}(t_d/t_u)$

然后我们得到了runup过程计数器的计数值 $N_u$ 和rundown过程计数器的计数值 $N_d$ ，于是我们可以消去时间，只用计数器的计数值就可以求解出输入电压:

 $Vin = -V_{ref}(N_d/N_u)$

双斜率积分ADC技术的美妙之处就在于它对于大多数的电路参数并不敏感！看看最终的表达式吧，如果我们想要精确地得到测量结果，我们只需要一个足够精准的Vref（基准电压源）和一个频率足够高（时间细度更小）的计数器！
更喵的一点是，这种架构可以牺牲采样速度来换取更高的采样精度！（改变电阻/电容就可以使runup和rundown的时间变长）

但是这种架构也是有缺点的。双斜率算法的主要问题是它的分辨率和速度是有上限的。一个双斜率ADC的测量时间是:

 $T_m = 2T_{ck}M$

Tm是理论上执行一次满量程测量的最小时间。Tck是ADC时钟的周期（也就是那个计数器的周期），M是满量程分辨率的计数值（比如24位是2的24次方）。即使使用20MHz的时钟，执行一次10000counts分辨率的测量也需要至少1ms（采样率就是1kHz），这个参数约等于采样率1kHz，分辨率为13.3位的ADC。

同时，宽带电路噪声和积分器的最高电压摆幅（约为±10V）同样限制了双斜率ADC的分辨率。宽带噪声决定了rundown过程结尾的过零点检测精度，想要检测1mV，甚至1uV的过零比较是难以实现的。所以这种算法受限于自身原因，最高分辨率能做到4-5位有效数字。（比如10V满量程，可分辨1mV）

更好的双斜率积分

我们可以简单地用一个额外的电阻让双斜率的采样速度直接翻倍。一个电阻用于runup,一个用于rundown。

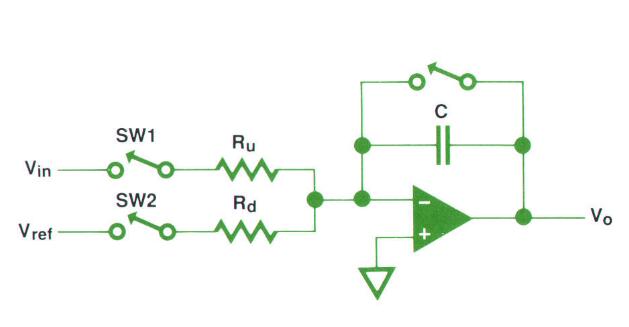
待测电压Vin连接到runup电阻Ru上，Ru是 远小于 rundown电阻Rd的，这样就会加快runup过程（积分电容充电），而减缓rundown过程（积分电容放电），这样就可以在不牺牲精度的情况下加速runup过程，加速比就是2电阻之比，Vin的测量结果可由下式计算:

 $V_{in} = -V_{ref}(N_d/N_u)(R_u/R_d)$

因为电阻网络可以精确匹配并且通过物理手段使其温漂保持一致，所以这种增强方法非常不错。

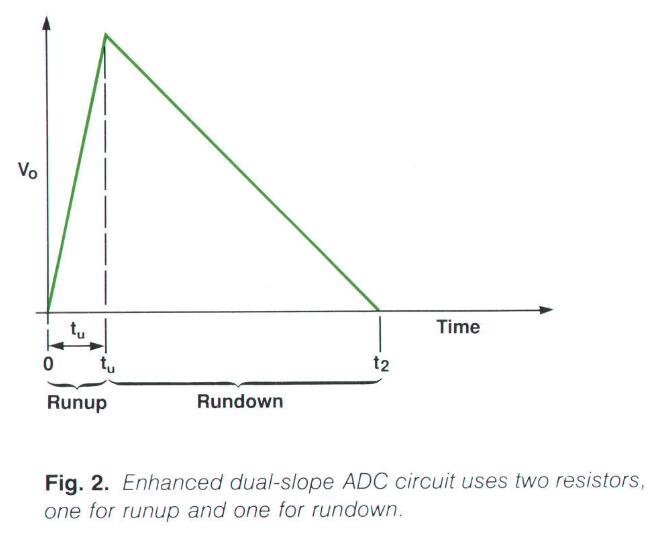
多斜率！

增强型双斜率缩短了runup所需的时间，而多斜率则是缩短了rundown的时间——
多斜率使用多个电阻来执行rundown操作，并且进行多次过零比较，可以简单理解为逐次逼近，每次都会更加精准。相比于使用单个电阻它的rundown时间更短。多斜率的电阻比例是 基于一个数 的，比如基2、基10。（下图是基10）

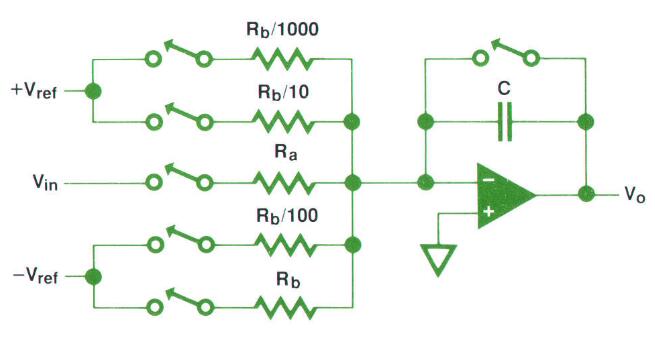
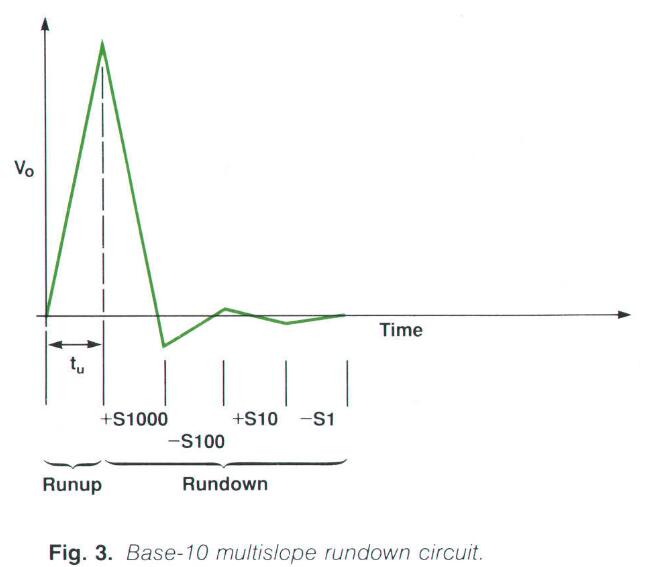
上面这个多斜率电路使用了 4个斜率，通过4个不同的电阻来实现，它们的权重分别是1000、100、10和1。根据每个斜率的极性（+Vref和-Vref）和比例大小，在波形图中标识了其符号（S)。比如说，S1000是一个一个时钟周期计数+1000次的正斜率，-S100是一个时钟周期计数-100次的负斜率。意思就是说在+S1000阶段，每一个时钟周期计数器将计数加1000个，在-S100阶段，每一个时钟周期计数器将减100个计数，如此往复逼近之后将得到一个最终稳定下来的计数值，这就是我们最终的、最精确的结果。

如果每一个斜率对应的曲线在过零之后的一个时钟周期后关闭，那么下一个斜率对应曲线应该需要额外的10个或以下个时钟周期来完成过零。那么，理论上完成rundown过程所需要的时间Td就是:

 $t_d < NBT_{ck}$

其中，N是斜率的个数，B是多斜率的比例基数。实际上，rundown要花费的时间会更长一些，因为不可能每次过零之后的一个时钟周期后就可以关断并切换至下一个斜率。考虑到这些延迟，最终花费的时间最大应该是:

 $t_d < kNBT_{ck}$

其中k是一个大于1的常数（废话）关掉一个斜率对应的充放电过程的时延导致了积分器的输出会产生 过冲（overshooting） 。对于每一个斜率曲线末端的时延对应的过冲，接下来的一个斜率曲线必须要经过 B 个时钟周期去平缓（安抚ww）这个过冲。k的典型值大概是2到4，上图的多斜率积分式ADC可以实现如下性能：

k=2，使用20MHz的时钟，以10000counts分辨率进行采样，完整的一个采样周期是4us，采样率约为250kHz。这比上面的Dual-Slope快了125倍。。。

更逆天的多斜率积分

通过选择合适的斜率倍率基数B，可以实现更快的多斜率积分测量。。请注意下式中的斜率个数N，也可以写成 $log_B(M)$ ，M是指定测量精度对应的rundown过程所需要的counts数。

 $t_d< kBlog_B(M)T_{ck}$

数学上的最优基底是常数 e，无关分辨率（数学是魔鬼！）。使用e作为上面例子的基底来完成多斜率积分，其他参数不变，可以将采样时间缩短至2.5us，又比之前以10为基底的快了60%。。。

多斜率积分也是有代价的，代价就是需要 超精密匹配的电阻网络，不然最终ADC的精度和线性度无法达到要求。同时多斜率积分也需要一个更复杂的控制电路去实现各种状态的检测、控制和切换。

多斜率runup

多斜率runup是一个用于提升ADC分辨率的改进技术。之前提到过，双斜率积分的分辨率受限于积分器的最高电压摆幅还有电路中的宽带噪声。多斜率runup可以让ADC拥有比 积分器物理限制的最高电压摆幅 高得多的 等效电压摆幅。

多斜率runup涉及到在runup过程中周期性地为积分器的输入中添加+Vref和-Vref电压（未知的输入电压Vin是一直加载的），以此来保证积分器的输出永远不会饱和。在这个过程中同样是使用计数器去记下Vref的等效充/放电时间，然后在rundown过程中用相应的时长来加/减去Vref，通过这种方法能得到高得多的分辨率。

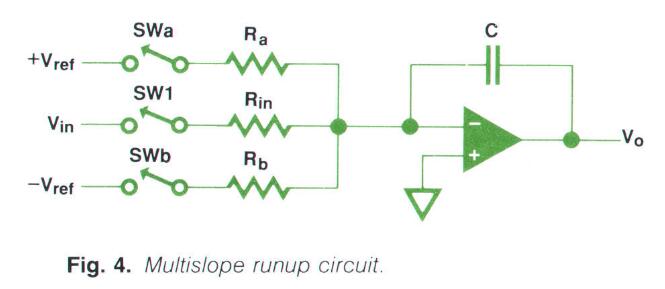
在Ra上加上+Vref，在Rb上加上-Vref，同样地通过开关控制2个Vref接入的时间，就可以精确地控制referenec为积分器充/放电的时间。下表列出了可能的4中runup过程中基准电压电流的情况。

需要注意的一点是，S+为积分器添加正积分量，S-为积分器添加负积分量。如果我们让S+和S-电流等大小反相，并且比满量程Vin输入所产生的电流稍微大那么一点点，那么基准电流总是能移除输入Vin所贡献的的积分量（如果基准电流比满量程Vin输入所产生的电流小，那么2个电流最终体现出来的还是为积分器充电，无法降低积分器的输出）。因此，这种方法就可以避免积分器输出饱和，通过周期性地检测积分器输出的极性，然后根据当前的极性相应地加入/减去S+和S-分量，就可以将积分器输出强制限制在0附近振荡。

Fig.5是一个典型的多斜率runup波形，带箭头的虚线是普通runup的波形，可以看出它很容易就会饱和。而绿色的曲线就是使用了Multi-Slope的runup波形，优点显而易见。

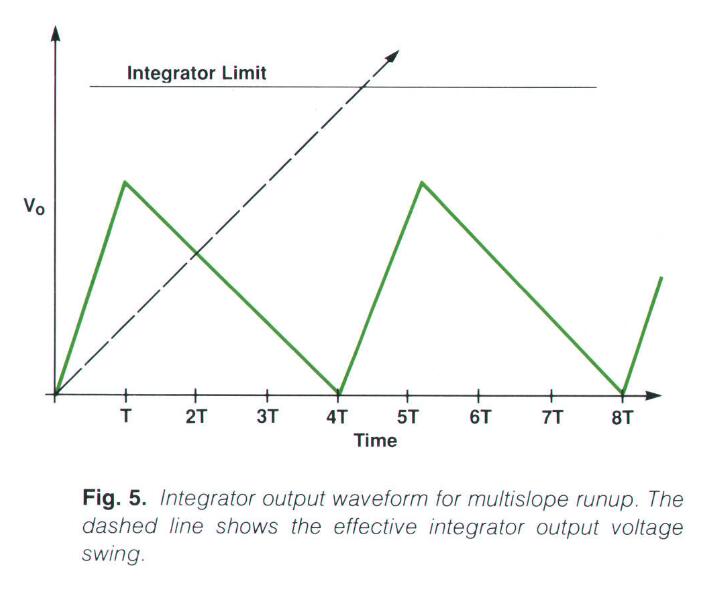
多斜率runup算法相比于双斜率runup有以下几点好处:

runup可以 持续任意长时间，因为积分器不会饱和。不过需要足够的计数器位数去存储计数数据。
可以在runup和rundown两个过程中同时提高精度，HP 3458A就是在runup过程中解析4位半精度，再在rundown过程中解析另外4位精度，实现了8位半精度。

对于任何一个ADC来说，线性度（Linearity） 都是一个极为重要的指标。但是多斜率runup算法并没有很好的线性度，因为每次开关都会为积分器传入一个 不可预测 的充电量/放电量，下图显示了2个应该为积分器传入同样电荷量的波形，但是由于它们的开关次数不同，它们最终传入的电荷量也不一样。（下面的有2次重复开关动作，导致了本应一直上升的三角波被翻折下来。而上面只有一次。）

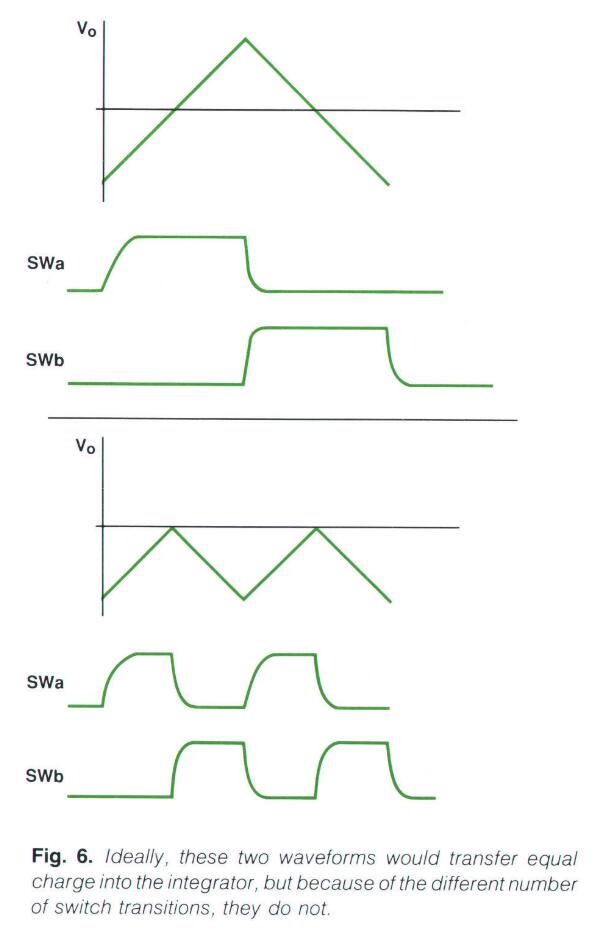
如果在每次转换时，使开关的开关次数为恒定值，那么无论输入信号是什么样的，这个问题都将不复存在。如果做到这点，那么每次转换的结果中都会有一个 offset。只要周期性地用一个零信号加载到输入上用来校准offset（读取零信号，得到的值就是offset，将这个值在后续每次读数中减去），就可以肥肠完美地解决这个问题。但要注意的是，必须周期性地去执行校准操作，因为开关的上升/下降时间是随温度而变化的，必须要确保校准数据和读数操作在同一温度附近，校准数据才有意义。

多斜率runup算法可以通过在每一个runup斜率上交替地施加恒定个开关周期时长的 S+0 和 S-0 信号来实现，下图展示了任意2个 S0+ 斜率之间的 4 种可能的斜率模式。不同的ADC输入电压会导致多斜率runup算法在这4种模式中切换。但无论是哪种模式，每个开关周期仅仅在第一个 S+0 斜率和 S-0 斜率之间传入一次电荷，并且在 S-0 斜率和下一个 S+0 斜率之间传入另一个。

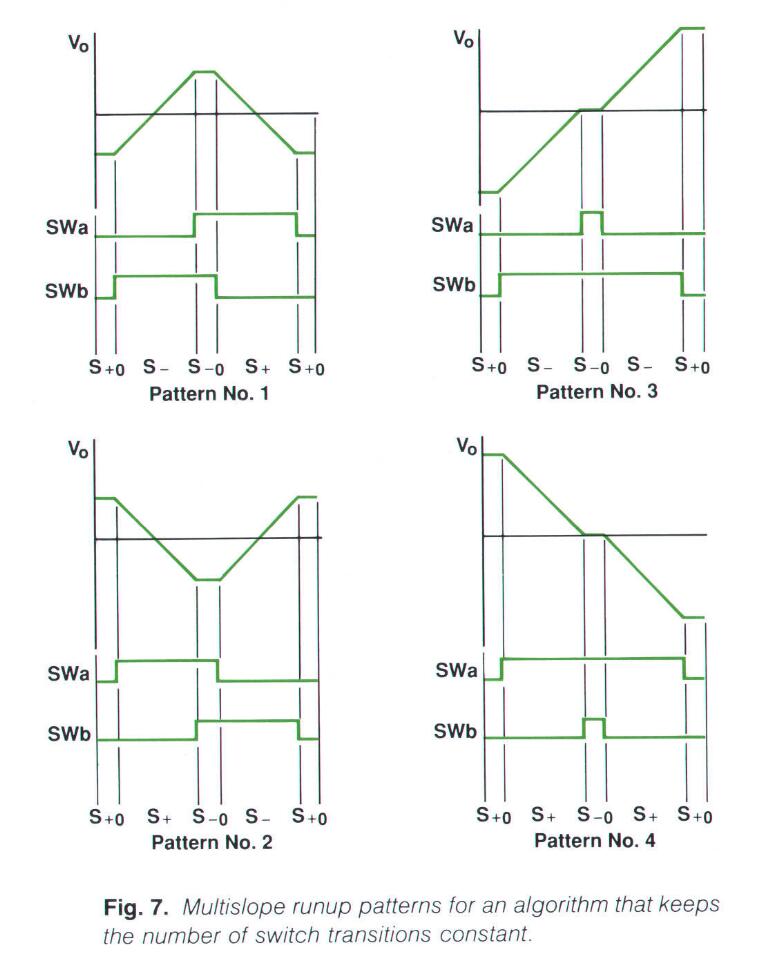
多斜率runup算法的开销相对来说比较小，多斜率runup的斜率可以和多斜率rundown的第一个斜率保持相同的权重。所以，只需要添加相反极性的斜率，以及相应的逻辑组件就可以完成这个算法。

HP3458A ADC Design

HP3458A的ADC设计就是基于以上描述的多斜率积分型ADC理论知识。设计ADC时，我们需要考虑如何去控制ADC、如何选择斜率比例基数、积分器能做到多快、线性度能做到多高，以及为积分器输入多大的电流（电阻的大小）等许多许多因素。。。需要同时兼顾ADC的高速和高精度，属实是项困难的工作。比如说如果需要实现高速，那么斜率就需要选得非常大以缩短总积分时间，但是这样一来积分器的非线性度就大幅增加，从而导致精度降级。

一个最简单的决策是选择多斜率rundown的比例基数。用数学常数e可以实现最高的速度，但是如果选择了e，那么ADC的输出就比较困难，因为ADC最终输出的是binary（二进制）。用2或4是非常适合binary系统的，并且它们都接近e。实际上用2或4当比例基数的转换速度是同等的，大致比e慢了百分之六左右，但是基2需要用2倍多的斜率去实现同样的精度，这样会导致硬件复杂度增加。因此选择4作为基底是比较经济合适的选择。

一般我们会用微处理器去控制多斜率ADC，但是HP3458A的速度要求扼杀了用微处理器作为主控的可能性。ADC的时钟预期是10MHz到20MHz之间，如果要在这种速度下做复杂的逻辑切换，微处理器是难以满足的。（1989年只有80C51，主频才12M...就算放到今天，要想在执行一堆复杂的判断时同时让微处理器的IO翻转速率达到20MHz也并不是一件容易的事情）所以，我们需要专用的硬件电路去控制ADC。因此，HP采用了Gate Array（FPGA或CPLD）实现了一个运行在20MHz的状态机，去控制ADC。ADC控制逻辑和积分器功能大约消耗了6k个CMOS门阵列。还需要另外的门阵列去实现计数器和触发控制，并且跑一个UART接口（2Mbits/sec），通过光纤将数据传输到数据处理和控制单元。

斜率的个数以及每个斜率的电流大小则是更为微妙的选择。如果斜率对应的电流过大，它将让积分器的输出级——运放不堪重负，从而导致严重的非线性。如果斜率对应的电流太小，开关和运放的漏电流可能会比最小的斜率对应的电流还要大，这样该斜率对应电流就无法让积分器的输出降至0。我们要确保最小的斜率对应的电流不小于1微安（1uA）来避免漏电流的影响。同样的，我们可以确信在5到6位半精度时，积分器可以承担起几mA（毫安）的输入电流，但是如果需要最高的精度和线性度（7位、8位半），我们必须要求输入电流小于1mA。而另一方面，如果需要实现高速，那么我们可能需要更大的输入电流（1mA以上）。因此，我们选择了2输入的ADC架构。

如下图所示，当执行高速测量时，输入电压通过10k电阻加载，这时是ADC的最大斜率，输入电流可能超过1mA。当执行高精度测量时，输入电压通过50k电阻加载，同样是最大斜率，但是此时输入电流必定小于1mA。最大斜率是S1024，对应电流1.2mA。总共有6个不同斜率（S1024,S256,S64,S16,S4和S1），其中S1的电流是1.2uA。S1024和S256都用于多斜率runup过程，因此无论是runup还是rundown，正负极性都存在。±S256斜率（0.3mA）用于通过50k电阻加载时，当输入通过10k电阻加载时，同时使用±S1024和±S256斜率并联（共1.5mA）。S256斜率比使用50k电阻作满量程输入时还要高出百分之25，这样可以避免积分器输入饱和。10k输入比50k输入要强5倍，因此同时使用S1024和S256，可以使用比最高斜率高25%的斜率用于高速转换。

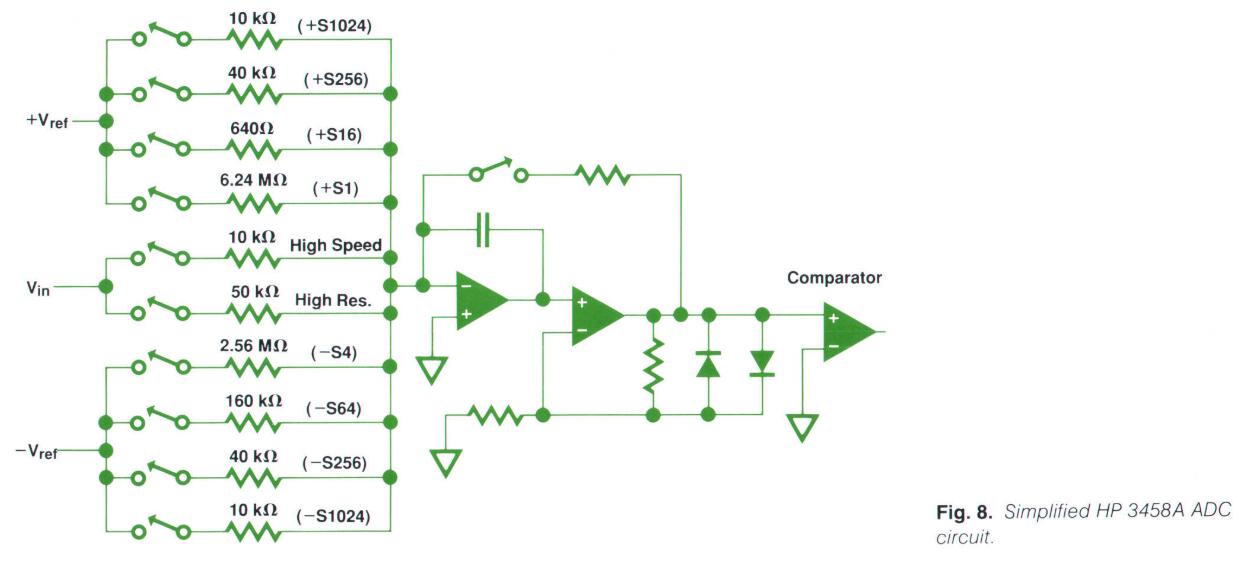
积分器

当最陡峭的斜率对应的压摆率逼近积分器的运算放大器的压摆率时，积分器的非线性度会增加。有2个影响积分器的压摆率的因素：

积分器总输入电流
积分器的积分电容大小

如果想要保持积分器的压摆率在10V/us以下，那么需要一个330pF的积分电容。这个积分电容必须具有 非常小的 介电吸收性，因为每次充电只需50fC（50飞库伦）

积分器电路需要对基准电流的变化做出快速响应，积分器的积分值在下一次可能的开关切换前要稳定到目标期望值的±0.01%区间内（整个过程约200ns）。同时积分器必须具有超低的电流/电压噪声，大约100V/us的压摆率、直流增益至少为25000，直流offset电压5mV、偏置电流小于10nA。有必要自行设计一个运算放大器来实现这所有的指标。。。

电阻网络

电阻网络有几个关键需求。最严格的需求是要求有极低的 温漂比例失配系数。因为ADC的增益和斜率比例系数和大小都由电阻网络的比例严格控制，如果电阻网络的比例随温度变化严重，那么ADC将不存在精度可言。HP3458A上的ADC电阻网络总共的温漂失配系数约为0.4ppm/°C（4千万分之一/每摄氏度）。即使是做到了如此恐怖的境地，如果电阻网络的温度有0.1度的变化，也将会在满量程8位半模式下ADC的最终读数中呈现出5 counts的跳动。（自动校准使得该系数可以小于0.15ppm/°C）。

对电阻网络的另一个需求是拥有足够低的绝对温度系数，这样可以确保电阻网络的自加热不会为整个系统贡献额外的非线性度。比如说，50k的输入电阻的输入电压范围是-12V到+12V。输入为0V和输入为12V时，电阻消耗的功率差值是2.88mW（毫瓦）,电阻消耗的功率转换成热，致使电阻温度上升，就会为ADC的非线性度做贡献。比如说这个电阻的绝对温度系数是1ppm/°C，那么在8位半测量模式下，仅仅0.01°C的温度变化就会引起1 count的跳动误差。HP3458A中使用的电阻网络并没有显示出这种由于 自加热现象 而产生的非线性。（你们用了什么天顶星黑科技电阻啊...）

最后的需求是电阻网络必须在HP3458A的一生中保持恒定的比率——也就是我们常常说的 长期稳定性（long-term stability）。为了在高速测量时保持良好的线性度，最不济的比例误差是0.1%，这是个相对简单的指标。如果要使ADC在8位半分辨率时的差分非线性度小于0.02ppm，对电阻比例的容差仅仅需要3%。

开关

最后一个需要谨慎选择的是控制输入的开关（switches），因为这些开关和电阻串联，它们的参数也会影响到ADC的温度系数。HP自己定制了一颗IC来做这个功能，保证开关的特性跟电阻的阻值数量级相匹配，这样就保证了ADC对于开关的比例跟踪温度系数敏感，而对绝对温度系数不敏感，这样保证了开关器件在同一温度下的一致性。另一个定制IC的好处是开关的控制信号可以在驱动级之前被锁存，这样可以让控制信号和时钟重新同步，可以有效减小开关过程中的时钟抖动。最终体现出的结果就是减小了ADC的整体噪声。

性能

ADC的性能被一些非理想的性质所限制，通常ADC所标识的位数被微分线性度或者噪声所限制。（即使在测量结果中跳动几counts，看起来精度要比标称高一些，实际上是噪声的锅）。比如说HP 3458A的ADC标称可达到9位半精度，但实际上只做了8位半测量，（约3.几bit差距）因为第9位已经呈现出严重的噪声特性，跳动非常严重以至于无法读取准确的测量数，并且微分线性度大约为8位。因此，在标识一个ADC的速度和分辨率时，指明这些参数是在何种条件下是 可信的（reliable） 是非常重要的（事实上几乎所有芯片都需要这样标识）。下图展示了3458A的采样速度和采样精度之间的关系（假定噪声真有效值小于1count）

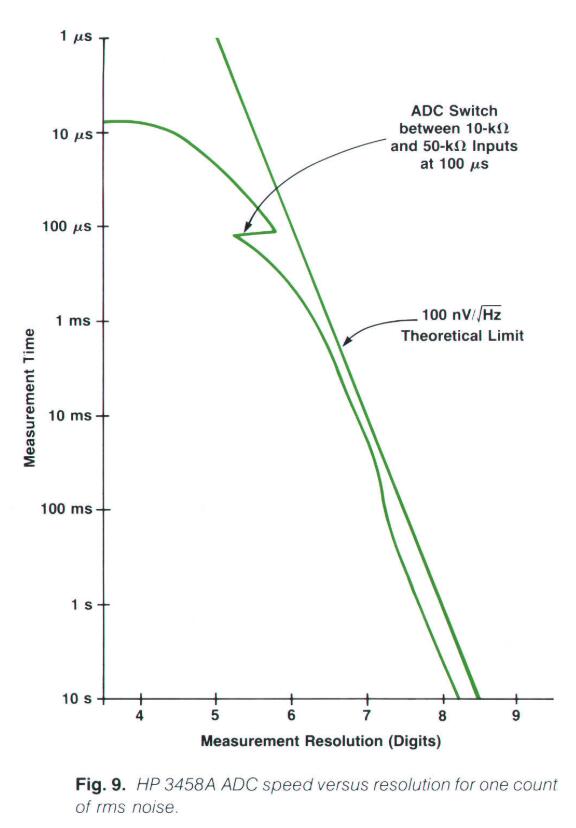
给定一个噪声值大小，就可以给出一个ADC在特定采样率下的分辨率极限。可以看出一个信号中高斯白噪声的带宽是一个时间T的积分：

 $BW = 1/2T.$

如果rundown不消耗时间，那么一个积分型ADC可以每T秒采样一次，在这个采样速率下，分辨率M受噪声限制为：

 $M = (V_{fs}\sqrt{2T})/V_n$

Vfs是ADC的满量程输入电压，Vn是高斯白噪声噪声的噪声密度，单位是V每根号Hz。下图表示了在100nV/根号Hz下，输入10V电压时，ADC的最高理论分辨率。3458A的表现非常接近一个工作在130nV/根号Hz高斯白噪声下的ADC的理论分辨率极限（靠近7位半区域）。在更低的分辨率区域，ADC的rundown时间在总共的转换时间中占比越来越高，因此降低了ADC的表现。在高分辨率时，ADC的1/f噪声会在测量周期内多次强制测量0信号用以降低噪声，提高精度至8位半精度，这同时降低了测量速率。

另一个评估ADC的性能的方法是画一个分辨率-积分时间图。积分时间指的就是runup的时间，见下图。

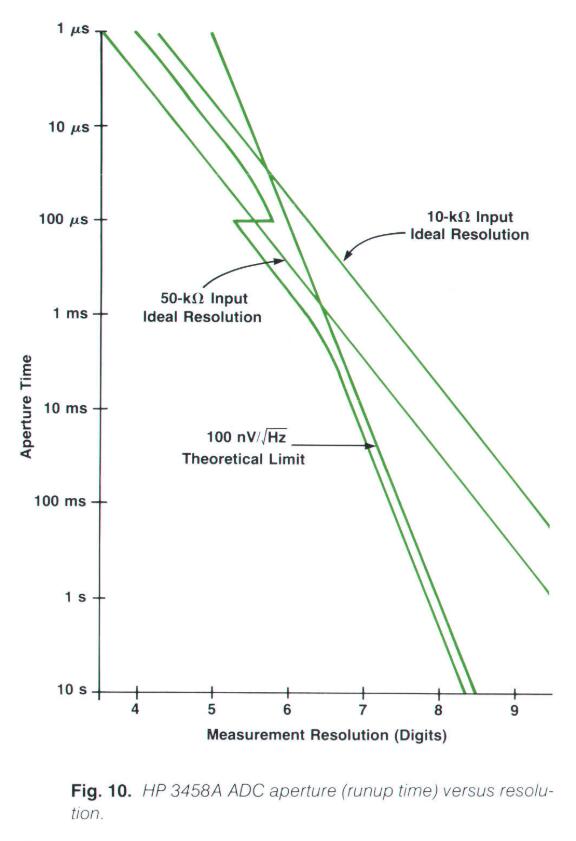
图中，有100nV/根号Hz的理论极限，还有ADC的理想无噪声分辨率曲线。在短积分时间区域内，3458A的分辨率远不如理论噪声极限，因为这时在rundown过程中检测最终的过零点将会带来大量的噪声（积分时间短），即多斜率积分算法并不能在这时达到理论极限。而如果把积分时间拉长，情况则会好很多。

线性度

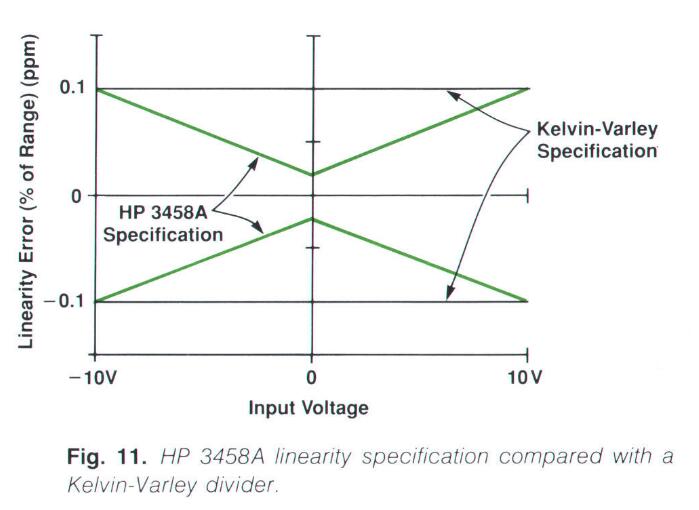
高精度线性度是ADC设计中的一个主要挑战。自动校准技术需要0.1ppm的积分线性度与0.02ppm的微分线性度。一个更重要的问题是如何测量、校验积分线性度。。（我们在做地球上最精密的ADC，用什么去校准呢？）最线性、且能用于商业用途的器件是 Kelvin-Varley divider。

我搜了搜，这种结构的分压器是目前地球上公认的精度最高的。。我还搜到一款Fluke公司生产的Kelvin-Varley 分压器，用于校准仪表。同时这种分压结构也可以用于制作最精密的DAC（数模转换器），看看这怪物的参数，0.1ppm精度，0.1ppm绝对线性度。。orz

校准线性度这部分挺复杂的，我暂时偷个懒不翻了）

以下是用Kelvin-Varley Divider和Josephson Junction Array联合测试出来的3458A线性度表现，可以看出，已经非常优秀了。

致谢

从15年前（1989-15=1974年）的HP 3455A 数字万用表开始，多斜率积分型ADC开始发扬光大，经过众多工程师和科学家的不懈工作后，将其推进至今天的高度。包括以下人员:

Advancement in Multisolpe ADC concepts
- Al Gookin
- Joe Marriott
- Larry Jones
- James Ressmeyer
- Larry DesJardin
Custom switch chip
- John Roe (from HP Colorado Intergrated Circuits Division)
Gate Array Development
- David Czenkusch
- David Rustici
Integrator Design
- Steve Venzke
U.S. National Bureau of Standards
- Clark Hamilton
- Dick Harris
- (for developing Josephson Junction Array Voltage System.)