本文目录
利用STM32的片上DAC实现DDS(数字频率合成)
前言
本篇文章参考了《新概念模拟电路-源电路与信号源》中的6.3节。
后续还会发布基于FPGA的DDS版本,敬请期待哦ovo
本文用到的资源
DDS
Direct-Digital Synthesizer是一种频率合成技术,用于产生周期性波形。目前,从低频到上百MHz的正弦波、三角波的产生,绝大多数都用DDS完成。包括我们买到的信号源之类的,里面的核心也是DDS芯片。传统的模拟电路——即振荡器产生正弦、方波、三角波的方式在DDS面前都得叫大哥:D
DDS的优点有:
- 可精细选择输出频率,实现从低到高的频率选择。
- 可快速跳频,且可以保证相位连续,这在模拟电路方法中是难以实现的。
- 可实现正交输出,可实现相位设置
- 可实现正弦、三角波输出,配合比较器可实现同频同相方波输出
- 事实上,只要有波表,随便什么波形都能给你打出来。。(你甚至可以在示波器屏幕上看Badapple)
当然DDS也不是浑身是宝,他也有弊端:
- 在发出高质量的正弦波中,DDS无法实现超低失真度,这是最大的弊端。(因为是一个点一个点地突变,不可避免会引起非线性失真,即增加了高频谐波分量)
- DDS中使用的DAC位数不会很高(常见的14位),其积分非线性INL不可能做到很小,其次DDS一般采用普通DAC,没有为降低失真度做出更多考虑
- 目前DDS实现的正弦波输出,失真度一般只能做到-80dB左右。
DDS核心思想
先假设DDS有一个固定的时钟MCLK=36MHz。
要实现高精度的DDS,我们需要一个正弦波的相位-幅度表,且它应具有足够细密的步长,比如0.01°。那么一个完整的正弦波表就需要36000个点。
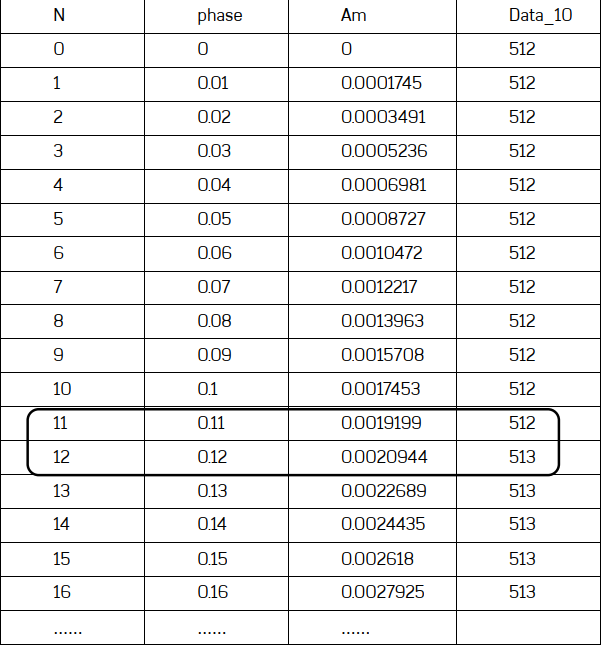
如上图所示,N代表相位点的序号,phase代表这个点对应的正弦相位,Am代表这个点对应的正弦的值(也就是sin(phase)),Data_10代表这个值对应的10位DAC的Code。
一个10位的DAC全幅度为1023,我们令code=1023时对应正弦的峰值,也就是1。code=0时对应正弦的谷值,也就是-1。所以正弦的值为0时,对应的code为512。
在前12个相位点,正弦的幅度变化非常小,以至于DAC输出的Code一直是512。在第13个相位点,DAC输出Code增加了1。由此可见这个具有36000点的波表几乎记录了一个标准正弦波的全部。
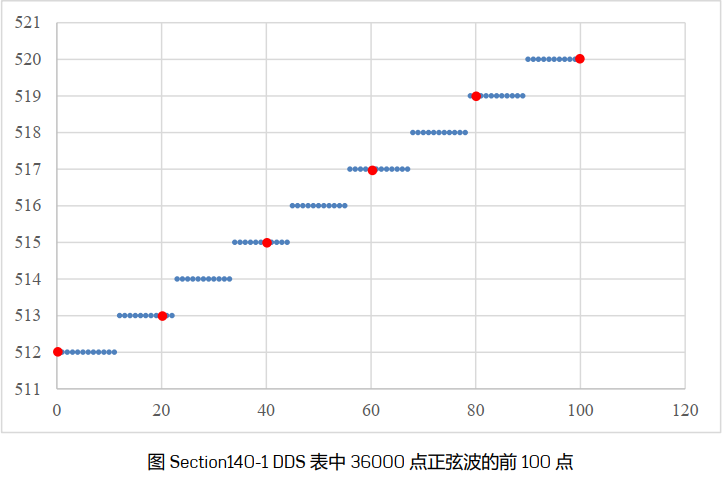
将这个表首位衔接,假设相位步长m=1,以DDS主时钟MCLK为节拍,依序发作:
- 第一个CLK时,DAC输出N=0时对应的DATA_OUT,即512.
- 第二个CLK时,DAC输出N=1时对应的DATA_OUT,即512
- ……
- 当36000个CLK过去之后,一个完整的正弦波便被打了出来。
之前我们假设DDS时钟为F_MCLK=36MHz
那么这个正弦波的频率就非常容易算出了:
f_{out} = {1 \over T_{MCLK}* {N_{max} \over m}} = {f_{MCLK}*m \over N_{max}} = {36*10^6*1 \over 36000} = 1000Hz
上式代表了DDS最核心的计算,参数含义如下:
- T_MCLK 为DDS主振荡器时钟周期,即1/36MHz,约为27.78ns。
- N_max为正弦波波表总点数,为36000
- m为循环增加中的步长,这里m=1,意味着逐个遍历整个表格。
如果m=2,意味着隔一个数据点扫一遍,那么此时输出信号的频率将翻倍。
m越大意味着间隔越大,扫描完的周期就越短,输出频率就越高。
可见,改变步长m就可以改变输出频率,当然,改变时钟频率也可以。不过一般采用固定的时钟。
那么DDS的最小分辨率就是:
\Delta f_{OUT} = {f_{MCLK}* \Delta m \over N_{max}}
根据上述参数确定的DDS输出最小分辨率为1000Hz。
实际DDS
前面假设的DDS主频不高,样点不多。
我们来看一个专用DDS芯片的内部框图。
AD9833是一款28位分辨率,25MHz完整DDS芯片。
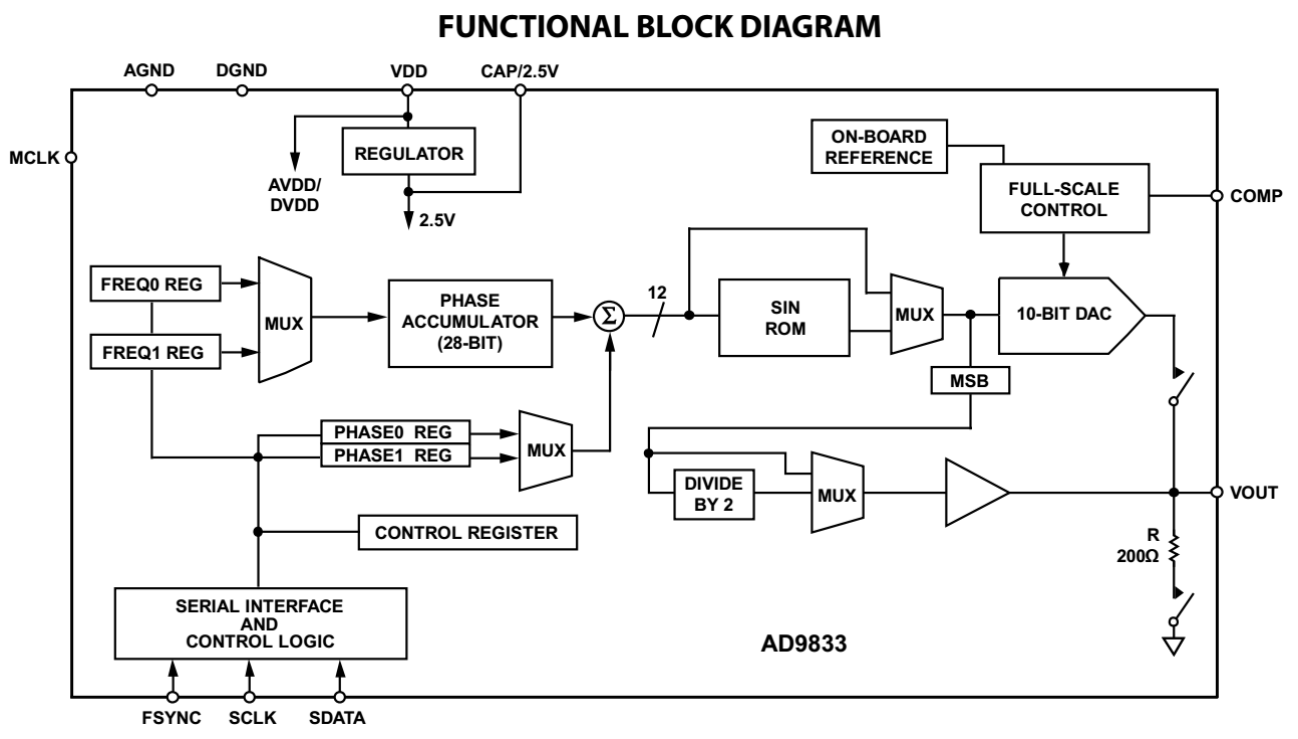
DDS核心由相位累加器PA、相位幅度表(波表)和数模转换器(DAC)组成。
对应上面的框图是这样的(好啦知道某些读者嘤语不好了orz):
- Phase accumulator(28-BIT)是28位相位累加器
- SIN ROM是只读存储器(Read-Only Memory),存储了正弦波表
- 10-BIT DAC就是10位数模转换器
- 其他的框图你可以暂时忽略不看~
28位相位累加器意味着什么呢?意味着它可以计数0~2^28,或者说,它的相位表点数为2^28=268435456点(2亿6800万),远远大于36000点。
如果我们要使用这个DDS,我们需要输入一个计数步长m(当然这个m小于2^28)。此后外部时钟MCLK每出现一个脉冲,相位累加器PA完成一次累加(以计数步长m为步进,在SIN ROM里等间隔抽值),DAC输出一个从正弦波表里抠出来的值。
那么这个DDS的最小频率分辨率是:
\Delta f = {1 \over 2^{28} }*f_{MCLK}= {25MHz \over 2^{28}} = 0.0931Hz多么恐怖的分辨率.jpg
也就意味着你可以设置这个DDS输出频率为10khz,10.0000931kHz,10.0001862kHz……
这个DDS输出的最高频率是FMCLK的一半。这时候整个波表中只有2个点会被扫描到,这时候输出的是一个三角波,而非正弦。
那么..32怎么做呢
斯密马赛,我们的STM32并不是DDS专用芯片,是存储不了如此恐怖的数据量(指超长波表)的。
那么我们从DAC的工作方式出发吧——
我们先解释方法,原因之后讲。
通常如果要使用STM32的DAC进行高速转换,我们需要用到DMA传输,数据流如下图所示:
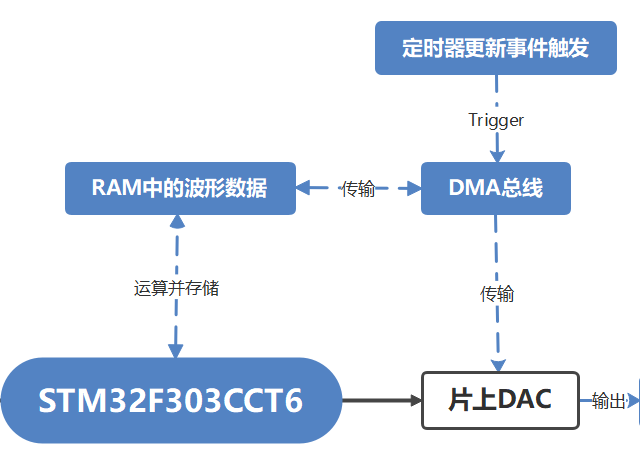
首先我们手搓一个波表出来(具体后面讲),然后把他存到RAM中(当然是RAM咯,实时运算出来的…),然后我们开启一个定时器,比如TIM8,配置成更新事件模式(Update Event)。
接下来,开启DMA传输,将DAC与DMA总线链接起来(Link),并指定DMA传输的源地址(source address),也就是我们存储在RAM里的波表数组的起始地址,同时指定DMA传输的长度(也就是波表长度)。
完成上述初始化操作之后,每当一个定时器更新事件出现时,DMA就会将一个波形数据点传输到DAC的输出保持寄存器中,过一会儿这个数据就会被自动装载到DAC的输出寄存器中,DAC便按这个数据进行相应的输出。
看到这里是不是明白了?我们将这个系统与前文的DDS对比一下:
- 定时器更新事件的频率 = DDS的主振荡器频率
- RAM中的波形数据长度 = DDS的波表长度
- 相位累加器步长m = 1,而DDS的m是可变的
为什么我们不用像真正DDS那样的固定波表呢?原因有2:
- STM32的DMA的 增量地址是连续的,也就是说DMA搬运数据时只能搬运地址连续的存储空间。
- STM32的存储空间有限,无法容纳如此巨量的数据。(毕竟是身娇体柔的单片机嘛)
那么我们如果需要一个可变长度的波表, 最好的办法就是现算现用 ,这样才能实现可调步长,也即实现输出频率可调。
并且,使用STM32有一个专用DDS芯片不太好实现的功能——可变时钟频率,只要更改定时器的更新事件触发频率,就改变了"DDS"的时钟频率。
那么我么来实践一下。
STM32的DAC
STM32的DAC在手册中注明了转换速率可达1Msps。但是这还不够—— 我们要更快!
参考这篇手册,Extending the DAC Performance of STM32 microcontrollers
文中提到了一件非常重要的事——STM32的DAC等效模型,以及为何DAC的输出速度提不上去
STM32的DAC等效模型
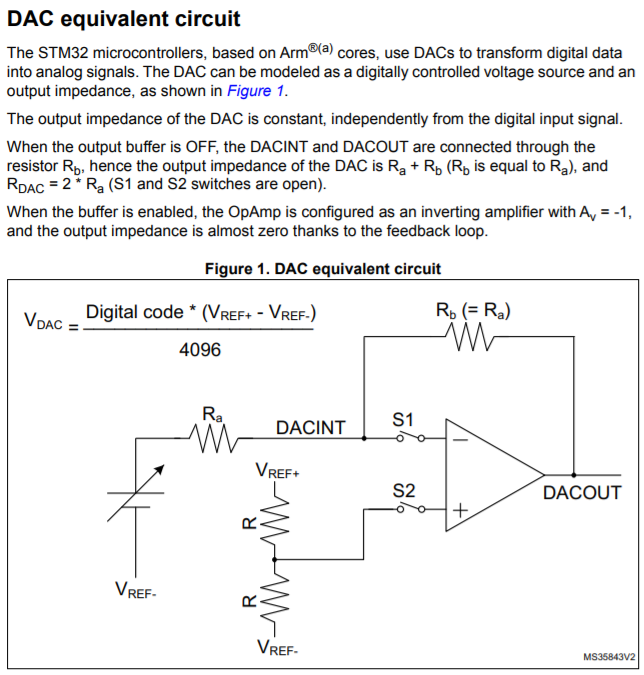
可以看到,当输出Buffer关闭的时候,DAC的等效输出阻抗为Ra+Rb,RDAC=2Ra。当输出Buffer开启时,一个内置的运放配置为反相放大模式,增益为-1,输出阻抗接近于0。(低阻)
但是当使用了输出Buffer的时候也带来了几个问题:
- 输出幅度被限制为正负电源轨±0.2V (因为这个运放并非轨到轨运放)
- 输出速度取决于这个运放的性能(通常只能到1MHz)
同时手册举了个例子,见下图:

简单来说,在输出Buffer关闭的情况下,如果输出有容性负载(事实上绝大多数情况下不可避免),如果要得到1LSB精度的输出值(也就是DAC输出稳定下来),通过RC充电电路的计算公式可以得出 DAC的Settling time。
算出来约为1.8us,也就是DAC的输出速率最高只能到 555kHz 左右!
而且这个计算还没考虑到DAC在高速运行时的其他寄生参数带来的影响,也就是说实际上这个最大速率会更低。
外部运放-提升性能
诶..我这么好的性能,怎么就速度上不去呢?(我没有开某人(bushi))
既然内部的Buffer太弟弟了,我们就外接一个牛逼点的。
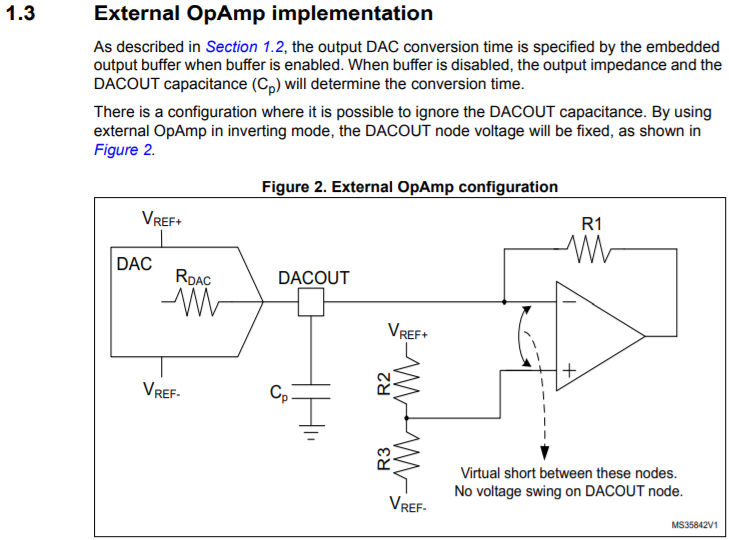
在这个模型中,限制DAC输出速度的主要有3个因素:
- RC常数
- 运放速度(压摆率,增益带宽积)
- DAC的数据更新率(主要是单片机限制)
当运用了外置运放之后,RC的影响就很小了,可以暂时忽略掉。现在对外置运放提出了要求——也就是高压摆率和高增益带宽积。(这个简单,氪金就行了。)
我使用了OPA2211,性能很牛的片子。
以下是我的电路图,用Kicad绘制。
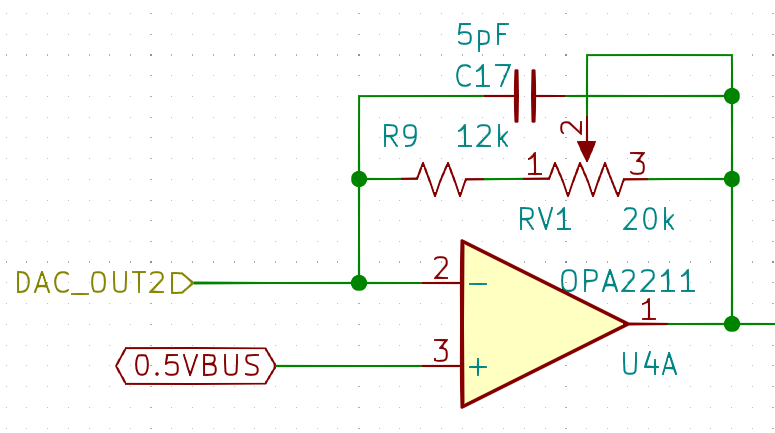
其中,0.5VBUS使用一个精密运放作为Buffer产生:
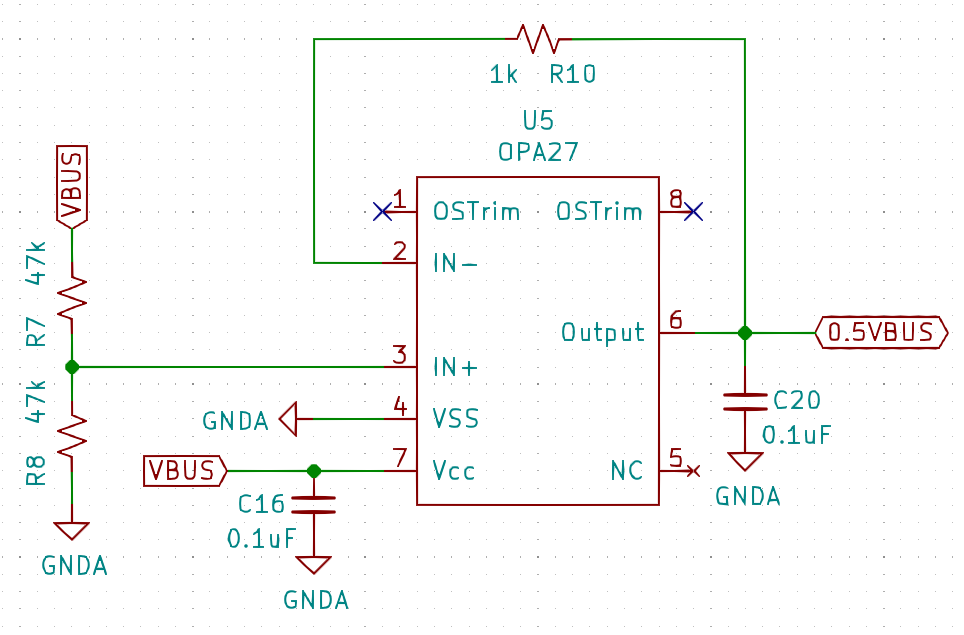
DAC的数据更新率
解决了RC和运放的问题,最后就是DAC的数据更新率了。
纵使我的外围硬件电路再牛逼,DAC的数据更新慢,输出频率一样上不去嘛。
先康康手册的描述:

有几种将数据传送到DAC的方法:
- 阻塞式,CPU将RAM中的数据搬运到DAC输出寄存器中(DOR
- 非阻塞式,利用DMA将CPU从繁重的苦力活里解放出来。DMA接管整个数据传输过程。
当然,我们是不希望CPU去当黑奴的,我们还要单片机干别的事情呢…
非阻塞情况下,我们使用定时器的更新事件去触发DMA搬运数据。所以数据更新率就取决于DMA总线的速度上限了。具体体现在以下几个参数:
- APB总线或AHB总线的时钟周期(视型号不同)
- DMA传输周期(从RAM到DAC的DOR寄存器)
- 定时器触发频率
比如STM32F407x的APB1总线上,当触发信号之后的3个周期,DHR中的数据被转移到DOR中,同时DMA产生请求,DMA花费至少一个时钟周期将数据搬运完成。
满打满算算下来搬运一个数据总共需要4个时钟周期。如果APB1总线频率42MHz,那么DAC的数据更新率能达到10.5Msps(M sample per second)。
当然这是F407的情况,别的型号具体还得查数据手册。
总之,DAC你还是蛮快的嘛(笑)
DMA Double Data Mode
还有一个小细节。

有些型号的DAC支持双数据模式。什么意思呢?
就是说DMA的总线是32-bit宽的,而DAC的数据是12-bit宽的,一般存储的话就使用uint16_t类型,是16-bit宽度。那么在DMA传输的时候,将2个数据一并传过去,占满DMA总线的位宽,可以提升2倍的数据速率(在定时器触发频率不变的情况下)。
当然,上限还是摆在那里的,这样做的意义是可以降低一半的定时器触发频率。
至此,我们找到了提升DAC输出速率的方法,从硬件到软件,从理论到实践,All Pass.
配置STM32
在CubeMx中配置STM32F303CCT6,这里就放最关键的配置啦,具体的可以看开头我传的工程文件~
配置DAC通道2,触发器选择 TIM8触发输出事件,同时禁用Buffer(具体为什么请看前文)

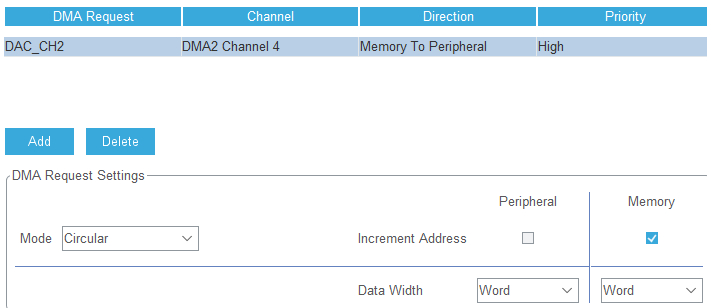
然后配置DAC的DMA通道:
- 选择DMA2_CHANNEL_4(我在网上看有人说F3的DAC只能用DMA2,我也没验证过DMA1能不能用…)
- Priority(优先级)设置为High
- Mode 选择 Circular(传输完成之后回到开头自动重新开始,即不间断传输)
- Data Width选择Word,即32位位宽,可以使用Double data Mode
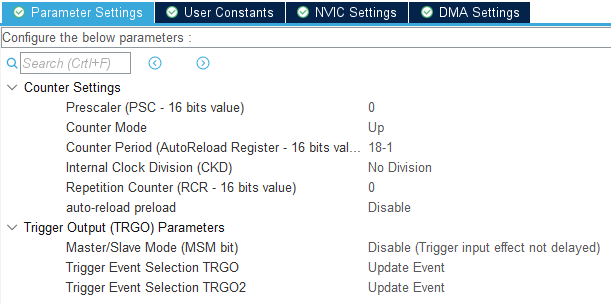
接下来是配置DAC的Trigger——TIM8
- Clock source选择Internal,查看时钟树可以看到TIM8的clock是72MHz
- 然后Prescaler(预分频)设置为0,不分频
- Counter Period(计数周期)设置为18-1那么定时器的触发频率就是 72MHz / 18 = 4MHz
- Trigger Event Selection TRGO选择Update Event,即更新事件,这个事件用于触发DAC的DMA去搬数据
别忘了,我们开了Double data Mode,定时器更新事件频率为4MHz,实际的DAC 输出 sampling rate应该是8MHz哦
生成波形算法
其实很简单,就是算。
比如以下是一个算正弦的例子
#define DAC_AMP (uint16_t)1600
#define LUT_MAX_LENGTH (uint32_t)4096
volatile uint16_t dds_lut[LUT_MAX_LENGTH];
if (type == SINE_WAVE)
{
float sin_step = 2.0f * 3.14159f / (float)(length-1);
for (uint16_t i = 0; i < length; i++)
{
dds_lut[i] = (uint16_t)(DAC_AMP+(DAC_AMP*sinf(sin_step*(float)i)));
}
}方波和三角波更为简单了,详细的请去文章开头的Git仓库看看吧~
测试!
输出200kHz的正弦波
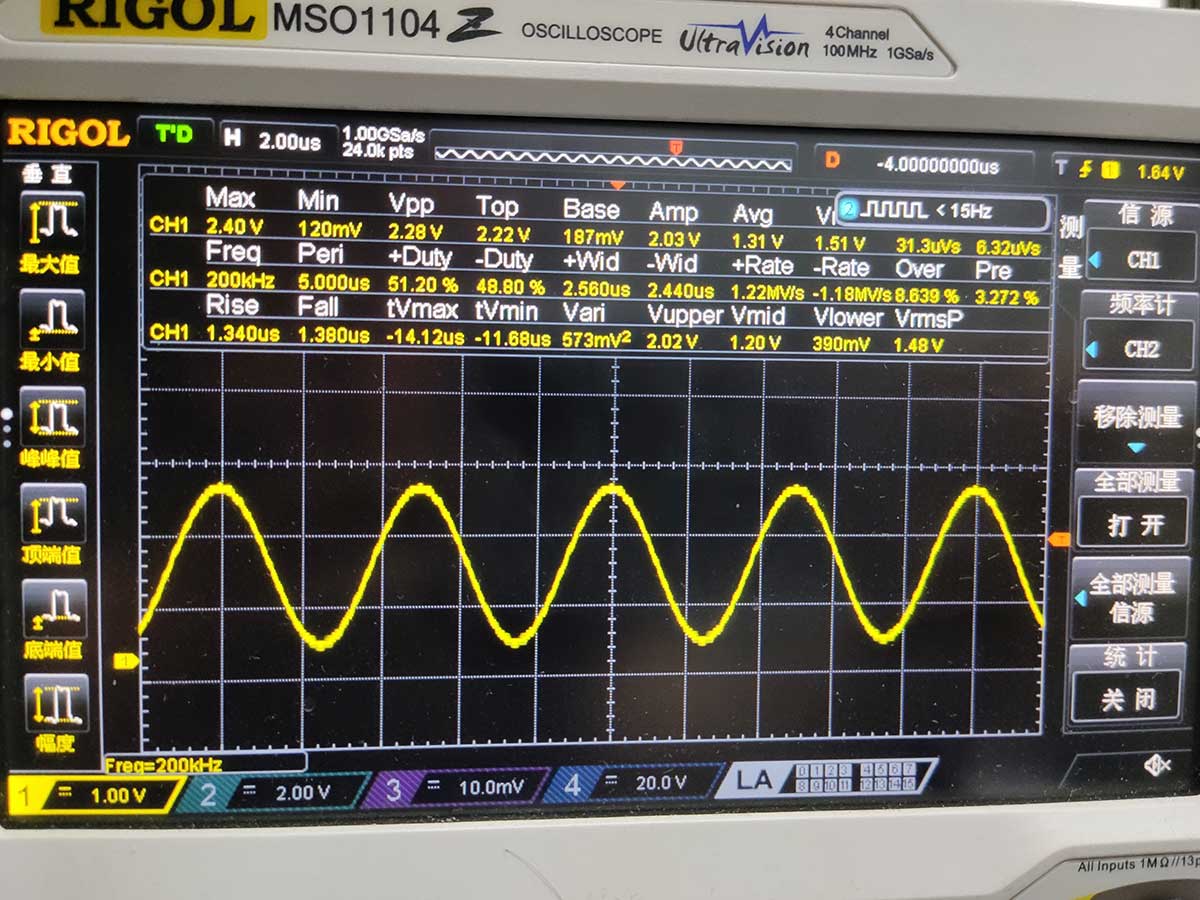
输出40kHz的正弦波+小板子合影
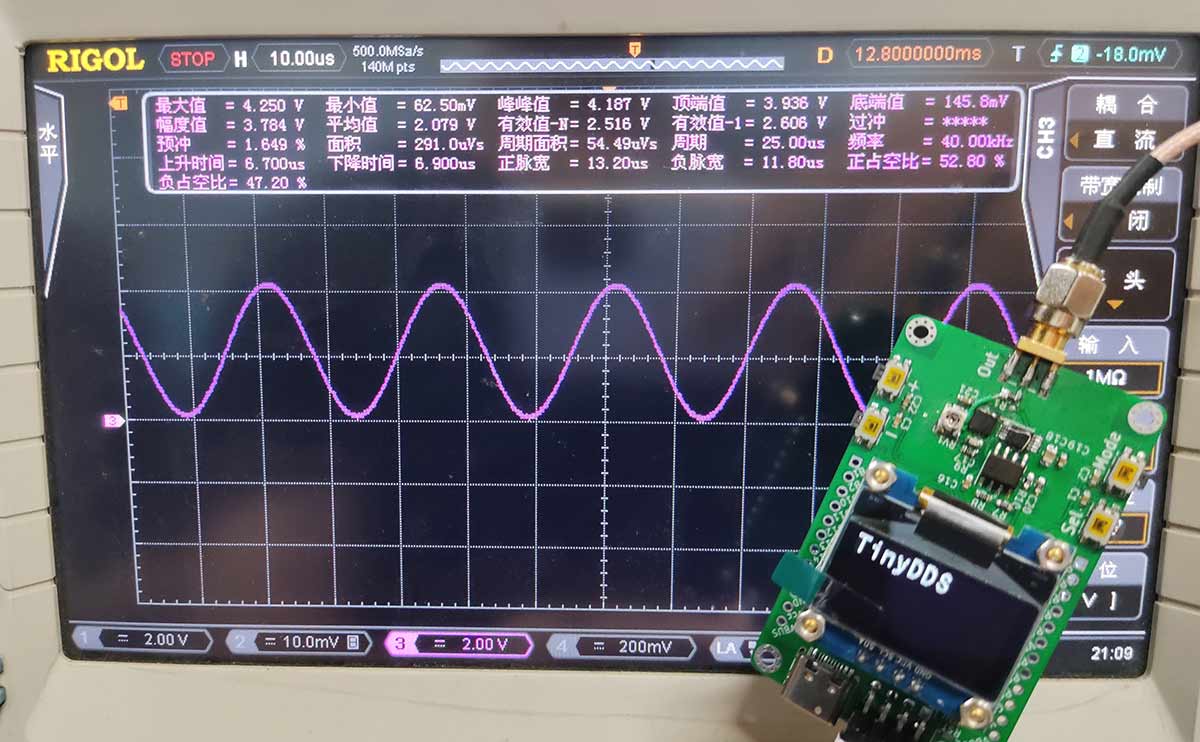
还有更多测试图,待后续上传.jpg




![[Bonjour STM32]No.番外-优雅地开发STM32](https://www.emoe.xyz/wp-content/uploads/2020/05/clion-1-logo-600x450.png)